
 如图,点E在BC上,点A、E、D在同一条直线上,AB⊥BC,CD⊥BC,若测得BE=20m,EC=10m,CD=20m,则河宽AB=( )
如图,点E在BC上,点A、E、D在同一条直线上,AB⊥BC,CD⊥BC,若测得BE=20m,EC=10m,CD=20m,则河宽AB=( )| A. | 60m | B. | 40m | C. | 30m | D. | 20m |
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:填空题
 我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.
我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
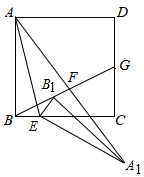 如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;
如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
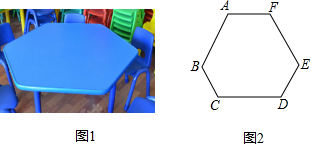
| A. | 640° | B. | 1080° | C. | 900° | D. | 720° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com