
 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A按顺时针方向旋转60°到△ADE的位置,连接BD并延长交AE于F.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A按顺时针方向旋转60°到△ADE的位置,连接BD并延长交AE于F.分析 (1)如图,作辅助线;首先运用勾股定理求出AB的长度;证明△ABE是等边三角形,进而证明B、D两点均在线段AE的中垂线上,得到∠BFA=90°,此为解决问题的关键性结论;运用直角三角形的边角关系即可解决问题.
(2)运用分割转化的数学思想,将阴影部分的面积转化为S扇形ABE与S扇形ADC的之差,借助扇形的面积公式,即可解决问题.
解答 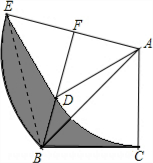 解:(1)连接BE.
解:(1)连接BE.
∵∠C=90°,AC=BC=$\sqrt{2}$
∴∠BAC=∠ABC=45°,$AB=\sqrt{A{C^2}+B{C^2}}=2$;
∵将△ABC绕点A按顺时针方向旋转60°得到△ADE,
∴AE=AB=2,DE=AD=AC=$\sqrt{2}$,
∠BAE=∠CAD=60°,∠DAE=∠BAC=45°;
∴△ABE是等边三角形,
∴AB=BE,
∴B、D两点均在线段AE的中垂线上,
∴∠BFA=90°,
∴DF=AD•sin∠DAE=1,BF=AB•sin∠BAE=$\sqrt{3}$,
∴BD=BF-DF=$\sqrt{3}-1$.
(2)由旋转变换可知,△ABC≌△AED,
∴S△ABC=S△AED,
∴S阴影=S扇形ABE+S△ABC-S△AED-S扇形ADC
=S扇形ABE-S扇形ADC
=$\frac{60π•{2}^{2}}{360}-\frac{60π•(\sqrt{2})^{2}}{360}$
=$\frac{4}{6}π-\frac{2}{6}π$
=$\frac{1}{3}π$.
点评 该题主要考查了旋转变换的性质、勾股定理、扇形的面积公式等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用旋转变换的性质、勾股定理、扇形的面积公式等几何知识点来分析、判断、解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
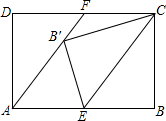 如图,已知矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B′处,连接AB′并延长交CD于点F.
如图,已知矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B′处,连接AB′并延长交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
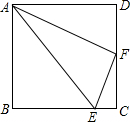 已知,如图,在正方形ABCD中,F是边CD的中点,点E在BC上,且AE=AD+CE.
已知,如图,在正方形ABCD中,F是边CD的中点,点E在BC上,且AE=AD+CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,整个阴影部分的面积9π-12$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,整个阴影部分的面积9π-12$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
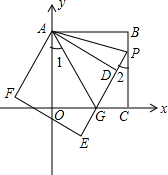 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
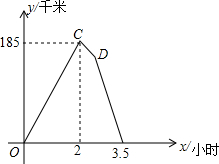 下面的图象反映的过程是:
下面的图象反映的过程是:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我省中学生的视力情况 | |
| B. | 了解九(1)班学生校服的尺码情况 | |
| C. | 检测一批电灯泡的使用寿命 | |
| D. | 调查台州《600全民新闻》栏目的收视率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com