
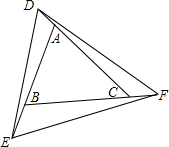
 如图所示,已知△ABC,延长CA、AB、BC到D、E、F,连接DE、EF、FD,使得∠AED=∠BFE=∠CDF.若∠ABC=60°,∠DFE=50°,求∠BAC及∠EDF的度数.
如图所示,已知△ABC,延长CA、AB、BC到D、E、F,连接DE、EF、FD,使得∠AED=∠BFE=∠CDF.若∠ABC=60°,∠DFE=50°,求∠BAC及∠EDF的度数.  波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
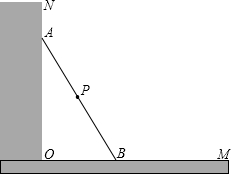 如图所示,一根长3米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上.设木棍的中点为P.若木棍A端沿墙下滑.且B端沿地面向右滑行.
如图所示,一根长3米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上.设木棍的中点为P.若木棍A端沿墙下滑.且B端沿地面向右滑行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
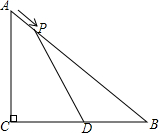 如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点.动点P从点A出发,沿着A→B方向以1cm/s的速度运动到点B停止运动.点P移动的时间为t秒,当△DBP为等腰三角形,求出t的值.
如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点.动点P从点A出发,沿着A→B方向以1cm/s的速度运动到点B停止运动.点P移动的时间为t秒,当△DBP为等腰三角形,求出t的值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com