
如图,点P是等边△ABC外接圆⊙O上一点,在以下判断中不正确的是( )

A.当弦PB最长时,△APC是等腰三角形;
B.当△APC是等腰三角形时,PO⊥AC;
C.当PO⊥AC,∠ACP=30゜;
D.当∠ACP=30゜时,△BPC是直角三角形。
C.
【解析】
试题分析:A、如图1,当弦PB最长时,PB为⊙O的直径,则∠BAP=90°.
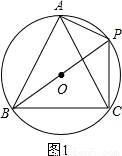
∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,AB=BC=CA,
∵点P是等边三角形ABC外接圆⊙O上的点,BP是直径,
∴BP⊥AC,
∴∠ABP=∠CBP=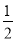 ∠ABC=30°,
∠ABC=30°,
∴AP=CP,
∴△APC是等腰三角形,
故本选项正确,不符合题意;
B、当△APC是等腰三角形时,分三种情况:
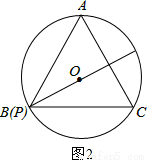
①如果PA=PC,那么点P在AC的垂直平分线上,则点P或者在图1中的位置,或者与点B重合(如图2),所以PO⊥AC,正确;
②如果AP=AC,那么点P与点B重合,所以PO⊥AC,正确;
③如果CP=CA,那么点P与点B重合,所以PO⊥AC,正确;
故本选项正确,不符合题意;
C、当PO⊥AC时,PO平分AC,则PO是AC的垂直平分线,点P或者在图1中的位置,或者与点B重合.
如果点P在图1中的位置,∠ACP=30°;
如果点P在B点的位置,∠ACP=60°;
故本选项错误,符合题意;
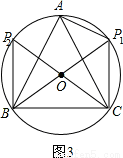
D、当∠ACP=30°时,点P或者在P1的位置,或者在P2的位置,如图3.
如果点P在P1的位置,∠BCP1=∠BCA+∠ACP1=60°+30°=90°,△BP1C是直角三角形;
如果点P在P2的位置,∵∠ACP2=30°,
∴∠ABP2=∠ACP2=30°,
∴∠CBP2=∠ABC+∠ABP2=60°+30°=90°,△BP2C是直角三角形;
故本选项正确,不符合题意.
故选C.
考点:1.三角形的外接圆与外心;2.等边三角形的性质;3.垂径定理;4.圆周角定理.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源:2014-2015学年云南省七年级上学期期中数学试卷(解析版) 题型:选择题
用字母 表示任意一个有理数,下列四个代数式中,值不可能为0的是( )
表示任意一个有理数,下列四个代数式中,值不可能为0的是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省九年级上学期期中考试数学试卷(解析版) 题型:填空题
某工厂利润两年间由45万元增加到88.2万元,工厂年利润的平均增长率为_______.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市七年级上学期第一次质量检测数学试卷(解析版) 题型:选择题
下列说法不正确的是 ( )
A.0既不是正数,也不是负数 B.1是绝对值最小的数
C.最大的负整数是 -1 D.0的绝对值是0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com