
如图,二次函数 (其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a;
(2))求证: 为定值;
为定值;
(3)设该二次函数图象的顶点为F.探索:在x轴的负半轴上是否存在点G,连接CF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.

(1) ;(2)证明见解析;(3)以线段GF、AD、AE的长度为三边长的三角形是直角三角形,此时点G的横坐标为-3m.
;(2)证明见解析;(3)以线段GF、AD、AE的长度为三边长的三角形是直角三角形,此时点G的横坐标为-3m.
【解析】
试题分析:(1)将C点代入函数解析式即可求得.
(2)令y=0求A、B的坐标,再根据,CD∥AB,求点D的坐标,由△ADM∽△AEN,对应边成比例,将求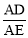 的比转化成求
的比转化成求 比,结果不含m即为定值.
比,结果不含m即为定值.
(3)连接FC并延长,与x轴负半轴的交点即为所求点G..过点F作FH⊥x轴于点H,在Rt△CGO和Rt△FGH中根据同角的同一个三角函数相等,可求OG(用m表示),然后利用勾股定理求GF和AD(用m表示),并求其比值,由(2)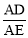 是定值,所以可得AD∶GF∶AE=3∶4∶5,由此可根据勾股定理逆定理判断以线段GF、AD、AE的长度为三边长的三角形是直角三角形,直接得点G的横坐标.
是定值,所以可得AD∶GF∶AE=3∶4∶5,由此可根据勾股定理逆定理判断以线段GF、AD、AE的长度为三边长的三角形是直角三角形,直接得点G的横坐标.
试题解析:【解析】
(1)将C(0,-3)代入函数表达式得, ,∴
,∴ .
.
(2)证明:如答图1,过点D、E分别作x轴的垂线,垂足为M、N.
由 解得x1=-m,x2=3m.∴A(-m,0),B(3m,0).
解得x1=-m,x2=3m.∴A(-m,0),B(3m,0).
∵CD∥AB,∴点D的坐标为(2m,-3).
∵AB平分∠DAE.∴∠DAM=∠EAN.
∵∠DMA=∠ENA=900,∴△ADM∽△AEN, ∴ .
.
设点E的坐标为(x,  ),
),
∴ ,∴x=4m.
,∴x=4m.
∴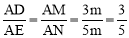 为定值.
为定值.

(3)存在,
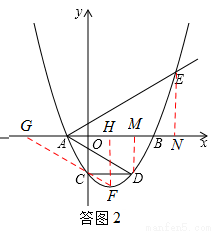
如答图2,连接FC并延长,与x轴负半轴的交点即为所求点G.
由题意得:二次函数图像顶点F的坐标为(m,-4),
过点F作FH⊥x轴于点H,
在Rt△CGO和Rt△FGH中,
∵tan∠CGO= , tan∠FGH=
, tan∠FGH= , ∴
, ∴ =
= .∴OG=3m,
.∴OG=3m,
由勾股定理得,GF= ,AD=
,AD=
∴ .
.
由(2)得, ,∴AD∶GF∶AE=3∶4∶5.
,∴AD∶GF∶AE=3∶4∶5.
∴以线段GF、AD、AE的长度为三边长的三角形是直角三角形,此时点G的横坐标为-3m.
考点:1.二次函数综合题;2.定值和直角三角形存在性问题;3.曲线上点的坐标与方程的关系;4.二次函数的性质;5.勾股定理和逆定理;6相似三角形的判定和性质;7.锐角三角函数定义.


科目:初中数学 来源:2014年初中毕业升学考试(江苏连云港卷)数学(解析版) 题型:选择题
一组数据1,3,6,1,2的众数与中位数分别是
A.1,6 B.1,1 C.2,1 D.1,2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:解答题
如图,已知函数 的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数 和y=x的图象于点C,D.
和y=x的图象于点C,D.
(1)求点A的坐标;
(2)若OB=CD,求a的值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:填空题
如图,在矩形ABCD中, ,以点B为圆心,BC长为半径画弧,交边AD于点E,若AE·ED=
,以点B为圆心,BC长为半径画弧,交边AD于点E,若AE·ED= ,则矩形ABCD的面积为 .
,则矩形ABCD的面积为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏淮安卷)数学(解析版) 题型:解答题
如图1,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.
(1)当t= 时,△PQR的边QR经过点B;
(2)设△PQR和矩形OABC重叠部分的面积为S,求S关于t的函数关系式;
(3)如图2,过定点E(5,0)作EF⊥BC,垂足为F,当△PQR的顶点R落在矩形OABC的内部时,过点R作x轴、y轴的平行线,分别交EF、BC于点M、N,若∠MAN=45°,求t的值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:填空题
如图,已知点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作 ABCD.若AB=
ABCD.若AB=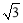 ,则
,则 ABCD面积的最大值为 .
ABCD面积的最大值为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com