
 如图,已知点A是第一象限内横坐标为2
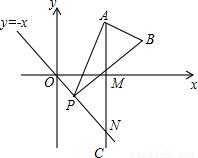
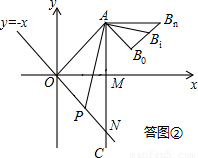
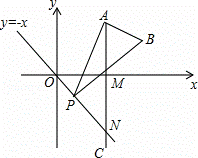
如图,已知点A是第一象限内横坐标为2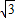 的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 . 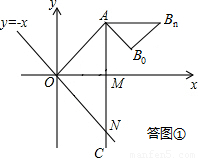 解:由题意可知,OM=
解:由题意可知,OM= ,点N在直线y=-x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,ON=
,点N在直线y=-x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,ON=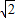 OM=
OM=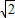 ×
×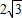 =
=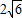 .
.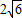 ×
×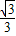 =
=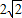 .
.
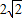 .
.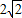 .
.

科目:初中数学 来源: 题型:
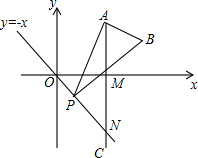 (2013•湖州)如图,已知点A是第一象限内横坐标为2
(2013•湖州)如图,已知点A是第一象限内横坐标为2| 3 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:浙江省月考题 题型:解答题
 和一次函数y=2x-1,其中一次函数图象经过(a,b)与(a+1,b+k)两点。
和一次函数y=2x-1,其中一次函数图象经过(a,b)与(a+1,b+k)两点。
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江湖州卷)数学(解析版) 题型:填空题
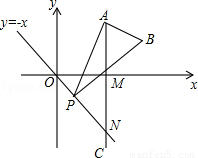
如图,已知点A是第一象限内横坐标为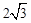 的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知点A是第一象限内横坐标为2![]() 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com