
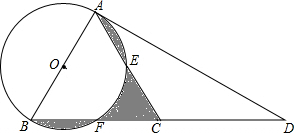
 如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F
如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F分析 (1)求出AC=BC=CD=$\frac{1}{2}$BD,即可求出∠BAD=90°,根据切线的判定得出即可;
(2)连接OE、AF、OF,分别求出等边三角形AOE、BOF、ABC的面积和扇形EOF的面积,即可求出答案.
解答 (1)证明:∵AC=BC,BC=CD,
∴AC=BC=CD=$\frac{1}{2}$BD,
∴∠BAD=90°,
即AD⊥BA,
∵BA过O,
∴AD是⊙O的切线;
(2)解: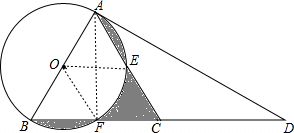
连接OE、AF、OF,
∵AC=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°,AB=BC=AC=12,
∵AB为直径,
∴∠AFB=90°,BF=FC=$\frac{1}{2}$BC=6,
在Rt△AFB中,由勾股定理得:AF=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$;
∴S△ABC=$\frac{1}{2}×12×6\sqrt{3}$=36$\sqrt{3}$;
∵OB=OF,∠ABC=∠BAC=60°,OA=OE,
∴△OBF、△AOE都是等边三角形,
∴OB=BF=OF=6,OA=OE=AE=$\frac{1}{2}$AB=6,∠AOE=∠BOF=60°,
∴∠EOF=180°-60°-60°=60°,
同法可求S△OBF=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$,
同理S△AOF=9$\sqrt{3}$,
∴阴影部分的面积是:S△ABC-S△BOF-S△AOE-S扇形EOF
=36$\sqrt{3}$-9$\sqrt{3}$-9$\sqrt{3}$-$\frac{60π×{6}^{2}}{360}$
=18$\sqrt{3}$-6π.
点评 本题考查了切线的判定,三角形的面积,扇形的面积的应用,能求出AB⊥AD和求出△ABC、△AOE、△BOF的面积是解此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
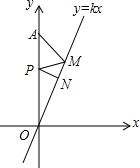 如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )
如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )| A. | 2 | B. | 4sin40° | ||
| C. | 2$\sqrt{3}$ | D. | 4sin20°(1+cos20°+sin20°cos20°) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
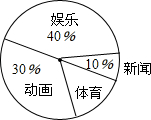 某校为调查1000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况,随机抽取了部分学生进行调查,并利用调查数据作出如图所示的扇形统计图.根据图中信息,可以估算出该校喜爱体育节目的学生共有( )
某校为调查1000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况,随机抽取了部分学生进行调查,并利用调查数据作出如图所示的扇形统计图.根据图中信息,可以估算出该校喜爱体育节目的学生共有( )| A. | 300名 | B. | 250名 | C. | 200名 | D. | 150名 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为一边在y轴的右侧作等边三角形OBC,将点C向左平移到点C′,且C′恰在AB上,求CC′的长.
如图所示,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为一边在y轴的右侧作等边三角形OBC,将点C向左平移到点C′,且C′恰在AB上,求CC′的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.
如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
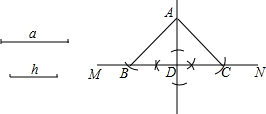
| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com