Question

1．平面直角坐标系中，直线y=3x+6与x轴、y轴分别交于点B、C，不论k为何值，直线l：y=kx-2k都经过x轴上点A
（1）如图1，若直线l过点C，求直线l的解析式和点A的坐标；
（2）如图2，将线段BC沿某个方向平移，点B、C对应的点M、N恰好在直线l和直线y=2x-4上，当k=1时，请你判断四边形BMNC的形状，并说明理由；
（3）如图3，点P由点C向下平移（6-2$\sqrt{3}$）个单位得到，点Q是x轴上的动点，以P、Q为顶点作菱形PRQT，且∠T=60°．直线l经过顶点R，当点Q在x轴上运动（点R不与点A重合）时，k的值是否会发生变化？若不变，求出k的值；若变化，请说明理由．

Answer 1

分析 （1）首先根据y=3x+6与y轴交于点C，可得点C坐标为（0，6）；然后将点C的坐标代入y=kx-2k，求出k的值，即可确定直线l的解析式，再求出点A坐标即可．
（2）首先根据平移的性质，可得四边形BMNC是平行四边形；然后求出点N的坐标，进而判断出NC=BC，即可判断出四边形BMNC是菱形，据此解答即可．
（3）首先连接AP、PQ，直线l交y轴于点H，再根据等边三角形的判定方法，判断出△PAB、△PQR等边三角形，然后在Rt△OAH中，根据∠OAH=60°，OH=OA•tan60°=2$\sqrt{3}$，求出k的值是多少，进而判断出k的值不会发生变化即可．

解答 解：（1）∵y=3x+6与y轴交于点C，
∴点C坐标为（0，6），
将点C的坐标代入y=kx-2k，可得
-2k=6，
解得k=-3，
∴直线l解析式为：y=-3x+6，
∴点A坐标为（2，0）；

（2）如图2，作NP⊥y轴于点P，，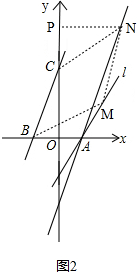
∵y=3x+6与x轴交于点B，
∴点B坐标为（-2，0），
∵y=3x+6与y轴交于点C，
∴点C坐标为（0，6），
当k=1时，y=kx-2k=x-2，
根据平移的性质，可得
四边形BMNC是平行四边形，
设点M坐标是（m，m-2），
则点N坐标是（m+2，m+4），
∵点N在直线y=2x-4上，
∴m+4=2（m+2）-4，
解得m=4，
∴m+2=4+2=6，m+4=4+4=8，
∴点N的坐标是（6，8），
∵NC=$\sqrt{{PN}^{2}{+PC}^{2}}=\sqrt{{6}^{2}{+（8-6）}^{2}}$=2$\sqrt{10}$，BC=$\sqrt{{OB}^{2}{+OC}^{2}}=\sqrt{{2}^{2}{+6}^{2}}=2\sqrt{10}$，
∴NC=BC，
又∵四边形BMNC是平行四边形，
∴四边形BMNC是菱形．

（3）如图3，连接AP、PQ，直线l交y轴于点H，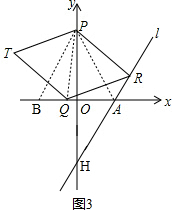
∵点C的坐标是（0，6），6-（6-2$\sqrt{3}$）=2$\sqrt{3}$，
∴点P的坐标是（0，2$\sqrt{3}$），
∴AP=$\sqrt{{OP}^{2}{+OA}^{2}}=\sqrt{{（2\sqrt{3}）}^{2}{+2}^{2}}$=4，
令点B的坐标是（-2，0），
则PA=PB=AB=4，
∴△PAB是等边三角形，
∴∠BPA=60°，
∴∠BPQ+∠QPA=60°；
∵∠PRQ=60°，PR=QR，
∴△PQR是等边三角形，
∴∠QPR=60°，
∴∠APR+∠QPA=60°，
又∵∠BPQ+∠QPA=60°，
∴∠APR=∠BPQ，
在△APR和△BPQ中，
$\left\{\begin{array}{l}{AP=BP}\\{∠APR=∠BPQ}\\{PR=PQ}\end{array}\right.$
∴△APR≌△BPQ，
∴∠PAR=∠PBQ=60°，
∴∠OAH=180°-∠PAO-∠PAR
=180°-60°-60°
=60°
∴OH=OA•tan60°=2$\sqrt{3}$，
∴2k=2$\sqrt{3}$，
∴k=$\sqrt{3}$，
∴k的值不会发生变化，k的值是$\sqrt{3}$．

点评 （1）此题主要考查了一次函数综合题，考查了分析推理能力，考查了分类讨论思想的应用，考查了数形结合思想的应用，考查了从已知函数图象中获取信息，并能利用获取的信息解答相应的问题的能力．
（2）此题还考查了直角三角形的性质和应用，以及勾股定理的应用，要熟练掌握．
（3）此题还考查了菱形的判定方法和性质的应用，要熟练掌握．