
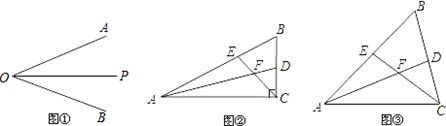
解:在OP上任找一点E,过E分别做CE⊥OA于C,ED⊥OB于D。如图①,
(1)结论为EF=FD。
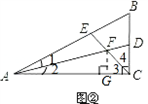
如图②,在AC上截取AG=AE,连接FG,
∵AD是∠BAC的平分线,
∴∠1=∠2,
在△AEF与△AGF中,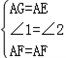 ,
,
∴△AEF≌△AGF(SAS),
∴∠AFE=∠AFG,FE=FG。
由∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,
∵2∠2+2∠3+∠B=180°,
∴∠2+∠3=60°,
又∠AFE为△AFC的外角,
∴∠AFE=∠CFD=∠AFG=∠2+∠3=60°,
∴∠CFG=60°,
即∠GFC=∠DFC,
在△CFG与△CFD中,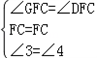 ,
,
∴△CFG≌△CFD(ASA),
∴FG=FD,
∴FE=FD;
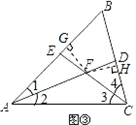
(2)EF=FD仍然成立。
如图③,过点F分别作FG⊥AB于点G,FH⊥BC于点H,
∴∠FGE=∠FHD=90°,
∵∠B=60°,且AD,CE分别是∠BAC,∠BCA的平分线,
∴∠2+∠3=60°,F是△ABC的内心,
∴∠GEF=∠BAC+∠3=60°+∠1,
∵F是△ABC的内心,即F在∠ABC的角平分线上,
∴FG=FH(角平分线上的点到角的两边相等),
又∠HDF=∠B+∠1(外角的性质),
∴∠GEF=∠HDF,
在△EGF与△DHF中,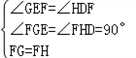 ,
,
∴△EGF≌△DHF(AAS),
∴FE=FD。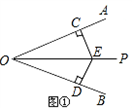


科目:初中数学 来源: 题型:
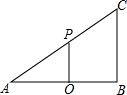 如图,在△ABC中,∠B=90°,AB=4,BC=3,O是AB的中点,OP⊥AB交AC于点P.
如图,在△ABC中,∠B=90°,AB=4,BC=3,O是AB的中点,OP⊥AB交AC于点P.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,矩形ABCD的长AB=5cm,点O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线y=ax2经过C、D两点,则图中阴影部分的面积是
如图,矩形ABCD的长AB=5cm,点O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线y=ax2经过C、D两点,则图中阴影部分的面积是| 25 |
| 32 |
| 25 |
| 32 |
查看答案和解析>>
科目:初中数学 来源: 题型:
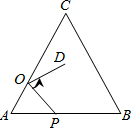 (2013•徐州模拟)如图,在等边△ABC中,AC=6,点O在AC上,且AO=2,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是
(2013•徐州模拟)如图,在等边△ABC中,AC=6,点O在AC上,且AO=2,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•黄陂区模拟)如图,PB为⊙0的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF
(2013•黄陂区模拟)如图,PB为⊙0的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,矩形ABCD的长AB=8cm,宽AD=3cm.O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线y=ax2经过C、D两点,则用图中阴影部分(整体)围成的圆锥的底面半径的长是
如图,矩形ABCD的长AB=8cm,宽AD=3cm.O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线y=ax2经过C、D两点,则用图中阴影部分(整体)围成的圆锥的底面半径的长是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com