110° 145°
分析:根据三角形的内角和定理求出∠ABC+∠ACB,再根据角平分线的定义求出∠DBC+∠DCB,然后在△BCD中,利用三角形的内角和定理列式求解饥渴得到∠CDB;
根据三角形的内角和定理以及角平分线的定义表示出∠DEG+∠DFG,然后根据四边形的内角和定理列式整理即可得解.
解答:∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°,
∵BE、CF分别是∠ABC和∠ACB的角平分线,
∴∠DBC=

∠ABC,∠DCB=

∠ACB,
∴∠DBC+∠DCB=

(∠ABC+∠ACB)=

×140°=70°,
在△BCD中,∠CDB=180°-(∠DBC+∠DCB)=180°-70°=110°;
∵EG,FG分别是∠AEB和∠AFC的角平分线,
∴∠DEG=

(180°-∠A-

∠ABC),
∠DFG=

(180°-∠A-

∠ACB),
∴∠DEG+∠DFG=

(180°-∠A-

∠ABC+180°-∠A-

∠ACB)=180°-∠A-

(∠ABC+∠ACB)=180°-40°-

×140°=105°,
又∵∠EDF=∠BDC=110°,
∴在四边形DEGF中,∠G=360°-105°-110°=145°.
故答案为:110°;145°.
点评:本题考查了三角形的内角和定理,三角形的角平分线的定义,四边形的内角和定理,要注意整体思想的利用.

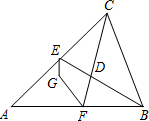 如图,在△ABC中,BE、CF分别是∠ABC和∠ACB的角平分线,并相交于点D,EG,FG分别是∠AEB和∠AFC的角平分线,并相交于点G,如果∠A=40°,那么∠CDB=________;∠G=________.
如图,在△ABC中,BE、CF分别是∠ABC和∠ACB的角平分线,并相交于点D,EG,FG分别是∠AEB和∠AFC的角平分线,并相交于点G,如果∠A=40°,那么∠CDB=________;∠G=________. ∠ABC,∠DCB=
∠ABC,∠DCB= ∠ACB,
∠ACB, (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ×140°=70°,
×140°=70°, (180°-∠A-
(180°-∠A- ∠ABC),
∠ABC), (180°-∠A-
(180°-∠A- ∠ACB),
∠ACB), (180°-∠A-
(180°-∠A- ∠ABC+180°-∠A-
∠ABC+180°-∠A- ∠ACB)=180°-∠A-
∠ACB)=180°-∠A- (∠ABC+∠ACB)=180°-40°-
(∠ABC+∠ACB)=180°-40°- ×140°=105°,
×140°=105°,

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为