
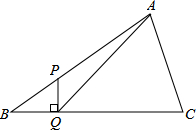
 如图,在△ABC中,∠B=30°,点P是AB上一点,AP=3BP,PQ⊥BC于Q,连接AQ,则cos∠AQC的值为$\frac{3\sqrt{129}}{43}$.
如图,在△ABC中,∠B=30°,点P是AB上一点,AP=3BP,PQ⊥BC于Q,连接AQ,则cos∠AQC的值为$\frac{3\sqrt{129}}{43}$. 分析 过A作BC的垂线AD,根据PQ⊥BC,∠B=30°可知BP=2PQ,BQ=$\sqrt{3}$PQ,故可得出△BPQ∽△BAD,再根据AP=3BP,可知AD=3PQ,DQ=2BQ=2$\sqrt{3}$PQ,进而可得出$\frac{AD}{DQ}$的值,设AD=$\sqrt{3}$x,则DQ=2x,由勾股定理可得出AQ的值,再由cos∠AQC=$\frac{DQ}{AQ}$即可得出结论.
解答 解:过A作BC的垂线AD,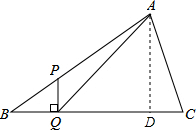
∵PQ⊥BC,∠B=30°,
∴BP=2PQ,BQ=$\sqrt{3}$PQ,
∵AD⊥BC,
∴△BPQ∽△BAD,
∵AP=3BP,
∴AD=4PQ,DQ=3BQ=3$\sqrt{3}$PQ,
∴$\frac{AD}{DQ}=\frac{4PQ}{3\sqrt{3}PQ}=\frac{4\sqrt{3}}{9}$,
设AD=$\sqrt{3}$x,则DQ=$\frac{9}{4}$x,AQ=$\sqrt{A{D}^{2}+D{Q}^{2}}=\sqrt{(\sqrt{3}x)^{2}+(\frac{9}{4}x)^{2}}=\frac{\sqrt{129}}{4}x$,
∴cos∠AQC=$\frac{DQ}{AQ}=\frac{\frac{9}{4}x}{\frac{\sqrt{129}}{4}x}=\frac{9\sqrt{129}}{129}$=$\frac{3\sqrt{129}}{43}$.
故答案为:$\frac{3\sqrt{129}}{43}$
点评 本题考查的是相似三角形的判定与性质,根据题意作出辅助线,构造出相似三角形是解答此题的关键.


科目:初中数学 来源: 题型:填空题
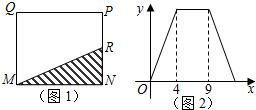 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图2表示变量y随x的变化情况,则当y=9时,点R所在的边是:PN边或QM边.
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图2表示变量y随x的变化情况,则当y=9时,点R所在的边是:PN边或QM边.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
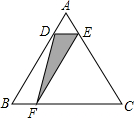 如图,在等边△ABC中,点D是AB边上的动点,过点作DE∥BC交边AC于点E,过点作EF∥AB交边BC于点F.连结DF,设动点D从点A出发沿AB匀速向点B运动,运动时间为t,则在整个运动过程中,△DEF的面积S与运动时间t的大致图象是( )
如图,在等边△ABC中,点D是AB边上的动点,过点作DE∥BC交边AC于点E,过点作EF∥AB交边BC于点F.连结DF,设动点D从点A出发沿AB匀速向点B运动,运动时间为t,则在整个运动过程中,△DEF的面积S与运动时间t的大致图象是( )| A. | 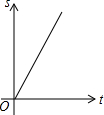 | B. | 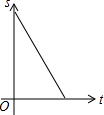 | C. | 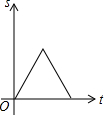 | D. | 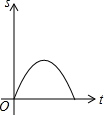 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
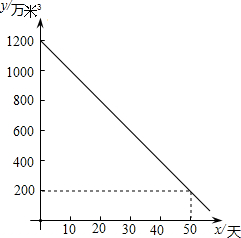 2013年8月由于持续高温和长时间无雨,南湖蓄水库的水量随着时间的增加而减少,干旱持续时间t天与蓄水量v(万立方米)的关系如图所示,回答下列问题:
2013年8月由于持续高温和长时间无雨,南湖蓄水库的水量随着时间的增加而减少,干旱持续时间t天与蓄水量v(万立方米)的关系如图所示,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
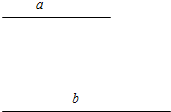 画图:已知线段a、b.
画图:已知线段a、b.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com