
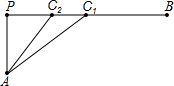
 如图,线段AP⊥PB,而且AP=2,PB=12,点C1,C2在线段PB上,满足PC2=1.5,BC1=6.设m=
如图,线段AP⊥PB,而且AP=2,PB=12,点C1,C2在线段PB上,满足PC2=1.5,BC1=6.设m=| AC2 |
| 3 |
| C2B |
| 5 |
| AC1 |
| 3 |
| C1B |
| 5 |
| A、m>n | B、m=n |
| C、m+n=5 | D、m<n |
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
 18、如图,PA、PB分别切⊙O于A、B,根据这些条件,你能得出哪些结论?(不再添字母和线段,半径相等除外,只写3个正确结论即可)
18、如图,PA、PB分别切⊙O于A、B,根据这些条件,你能得出哪些结论?(不再添字母和线段,半径相等除外,只写3个正确结论即可)查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 如图,线段AP⊥PB,而且AP=2,PB=12,点C1,C2在线段PB上,满足PC2=1.5,BC1=6.设
如图,线段AP⊥PB,而且AP=2,PB=12,点C1,C2在线段PB上,满足PC2=1.5,BC1=6.设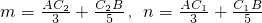 ,那么
,那么查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| AC2 |
| 3 |
| C2B |
| 5 |
| AC1 |
| 3 |
| C1B |
| 5 |
| A.m>n | B.m=n | C.m+n=5 | D.m<n |
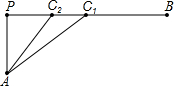
查看答案和解析>>
科目:初中数学 来源:2008年第4届“锐丰杯”初中数学邀请赛试卷(解析版) 题型:选择题
 ,那么( )
,那么( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com