

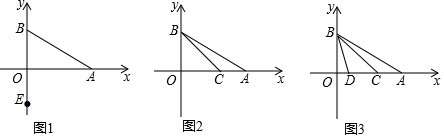
���� ��1���ɾ���ֵ��ż�η��ķǸ��ԣ����ɵó�b��c��d��ֵ��
��2�����˶�ʱ��Ϊt��ʱ����A��Ӧ����Ϊ2t-2����C��Ӧ����Ϊ12-t����A��C�����غϿɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
��3��������ڣ����˶�ʱ��Ϊt��ʱ����B��Ӧ����Ϊ2t����C��Ӧ����Ϊ12-t����D��Ӧ����Ϊ18-t����B��D�ľ�����C��D�ľ����3���ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
��� �⣺��1����|b|=0����c-12��2+|d-18|=0��
��b=0��c=12��d=18��
�ʴ�Ϊ��0��12��18��
��2�����˶�ʱ��Ϊt��ʱ����A��Ӧ����Ϊ2t-2����C��Ӧ����Ϊ12-t��
��������ã�2t-2=12-t��
��ã�t=$\frac{14}{3}$��
��tΪ$\frac{14}{3}$ʱ��A��C����������
��3��������ڣ����˶�ʱ��Ϊt��ʱ����B��Ӧ����Ϊ2t����C��Ӧ����Ϊ12-t����D��Ӧ����Ϊ18-t��
�ߵ�B�ڵ�D���Ҳ࣬��B��D�ľ�����C��D�ľ����3����
��2t-��18-t��=3[��18-t��-��12-t��]��
��ã�t=12��
�𣺴���ʱ��t��ʹ��B��D�ľ�����C��D�ľ����3������ʱt��ֵΪ12��
���� ���⿼����һԪһ�η��̵�Ӧ�á����ᡢ����ֵ�Լ�ż�η��ķǸ��ԣ�����Ĺؼ��ǣ���1�����ݾ���ֵ��ż�η��ķǸ������b��c��d��ֵ����2����A��C���غ��г�����t��һԪһ�η��̣���3����B��D�ľ�����C��D�ľ����3���г�����t��һԪһ�η��̣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
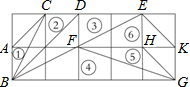 ��ͼ��ʾ������������������6��б�����Σ��١�ABC���ڡ�BCD���ۡ�BDE���ܡ�BFG���ݡ�FGH���ޡ�EFK���ڢڡ����У������������Ƶ��Тۢܢݣ�����ţ�
��ͼ��ʾ������������������6��б�����Σ��١�ABC���ڡ�BCD���ۡ�BDE���ܡ�BFG���ݡ�FGH���ޡ�EFK���ڢڡ����У������������Ƶ��Тۢܢݣ�����ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
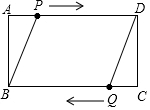 ��ͼ���ھ���ABCD�У�AB=4cm��AD=6cm����P�ӵ�A��������1cm/s���ٶ���AD���յ�D�˶���ͬʱ����Q�ӵ�C��������1cm/s���ٶ���CB���յ�B�˶������˶�ʱ��Ϊt��s����
��ͼ���ھ���ABCD�У�AB=4cm��AD=6cm����P�ӵ�A��������1cm/s���ٶ���AD���յ�D�˶���ͬʱ����Q�ӵ�C��������1cm/s���ٶ���CB���յ�B�˶������˶�ʱ��Ϊt��s�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
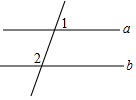 ��ͼ����ֱ֪��a��b����1=70�㣬��ô��2�Ķ����ǣ�������
��ͼ����ֱ֪��a��b����1=70�㣬��ô��2�Ķ����ǣ�������| A�� | 60�� | B�� | 80�� | C�� | 90�� | D�� | 110�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2 | C�� | x��2 | D�� | x��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com