
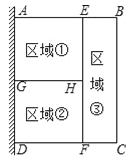
【题目】如图,某小区准备用篱笆围成一块矩形花圃ABCD,为了节省篱笆,一边利用足够长的墙,另外三边用篱笆围着,再用两段篱笆EF与GH将矩形ABCD分割成①②③三块矩形区域,而且这三块矩形区域的面积相等,现有总长80m的篱笆,当围成的花圃ABCD的面积最大时,AB的长为 m.
【答案】15.
【解析】
试题分析:根据三个矩形面积相等,得到矩形AEFD面积是矩形BCFE面积的2倍,可得出AE=2BE,设BC=x,BE=a,则有AE=2a,表示出a与2a,进而表示出y与x的关系式,利用二次函数的性质求出y的最大值,以及此时x的值,进而可得a的值,由AB=3a计算可得.
试题解析:∵三块矩形区域的面积相等,∴矩形AEFD面积是矩形BCFE面积的2倍,∴AE=2BE,设BC=x,BE=a,则AE=2a,∴8a+2x=80,∴a=![]() ,3a=
,3a=![]() ,∴y=
,∴y=![]() =
=![]() ,∵a=
,∵a=![]() >0,∴x<40,则y=
>0,∴x<40,则y=![]() =
=![]() (0<x<40),∴当x=20时,y有最大值,最大值为300平方米,当x=20时,a=
(0<x<40),∴当x=20时,y有最大值,最大值为300平方米,当x=20时,a=![]() =5,∴AB=AE+BE=3a=15米,故答案为:15.
=5,∴AB=AE+BE=3a=15米,故答案为:15.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
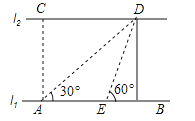
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
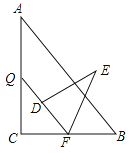
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长;
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com