
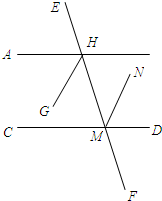
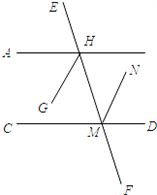
 如图,已知:HG平分∠AHM,MN平分∠DMH,且∠AHM=∠DMH.
如图,已知:HG平分∠AHM,MN平分∠DMH,且∠AHM=∠DMH. 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源:2012-2013年山西省农业大学附属中学七年级下学期第一次月考数学卷(带解析) 题型:解答题
(10分)完成下面的证明:已知,如图,AB∥CD,EG平分∠BEF,FG平分∠EFD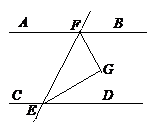
求证:∠EGF=90°
证明:∵HG∥AB(已知) ∴∠1=∠3( )
又∵HG∥CD(已知) ∴∠2=∠4( )
∵AB∥CD(已知) ∴∠BEF+___________=180°( )
又∵EG平分∠BEF(已知) ∴∠1=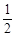 ∠______( )
∠______( )
又∵FG平分∠EFD(已知) ∴∠2=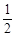 ∠ ( )
∠ ( )
∴∠1+∠2=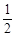 (___________+______________) ∴∠1+∠2=90°
(___________+______________) ∴∠1+∠2=90°
∴∠3+∠4=90°( )即∠EGF=90°
查看答案和解析>>
科目:初中数学 来源:2015届山西省七年级下学期第一次月考数学卷(解析版) 题型:解答题
(10分)完成下面的证明:已知,如图,AB∥CD,EG平分∠BEF,FG平分∠EFD
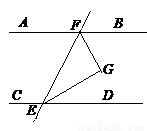
求证:∠EGF=90°
证明:∵HG∥AB(已知) ∴∠1=∠3( )
又∵HG∥CD(已知) ∴∠2=∠4( )
∵AB∥CD(已知) ∴∠BEF+___________=180°( )
又∵EG平分∠BEF(已知) ∴∠1=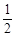 ∠______(
)
∠______(
)
又∵FG平分∠EFD(已知) ∴∠2=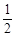 ∠ (
)
∠ (
)
∴∠1+∠2=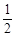 (___________+______________) ∴∠1+∠2=90°
(___________+______________) ∴∠1+∠2=90°
∴∠3+∠4=90°( )即∠EGF=90°
查看答案和解析>>
科目:初中数学 来源:湖北省期末题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com