
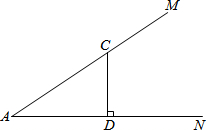
 如图,点C在∠MAN的边AM上,CD⊥AN,垂足为点D,点B在边AN上运动,∠BCA的平分线交AN于点E.
如图,点C在∠MAN的边AM上,CD⊥AN,垂足为点D,点B在边AN上运动,∠BCA的平分线交AN于点E.分析 (1)由三角形内角和定理可得∠ACB,由平分线性质可知∠ECB=40°,由三角形的内角和定理可得∠DCB;
(2)利用分类讨论的思想,情况一:β>α,情况二:β<α时,∠ECD=$\frac{1}{2}$α-$\frac{1}{2}$β;情况三:β=α时,∠ECD=0°;
解答 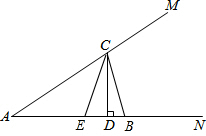 解:(1)如图,在△ABC中,
解:(1)如图,在△ABC中,
∵∠A=30°,∠B=70°,
∴∠ACB=80°,
∵CE平分∠ACB,
∴∠ECB=40°,
在△BCD中,
∵CD⊥AN,∠B=70°,
∴∠DCB=20°,
∴∠ECD=∠ECB-∠DCB=20°;
(2)情况一:β>α,
①β<90°时,∠ECD=$\frac{1}{2}$β-$\frac{1}{2}$α,
②β=90°时,∠ECD=$\frac{1}{2}$β-$\frac{1}{2}$α,
③β>90°时,∠ECD=$\frac{1}{2}$β-$\frac{1}{2}$α;
情况二:β<α时,∠ECD=$\frac{1}{2}$α-$\frac{1}{2}$β;
情况三:β=α时,∠ECD=0°;
综上所述,$∠ECD=\frac{|α-β|}{2}$.
点评 本题主要考查了三角形内角和定理和角平分线的性质,分类讨论是解题的关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com