练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

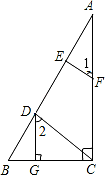
    已知：如下图，DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2，求证：CD⊥AB。
    证明：∵DG⊥BC，AC⊥BC（已知）
    ∴∠DGB=∠ACB=90°（垂直定义）
    ∴DG∥AC（    ）
    ∴∠2=（    ）（    ）
    ∵∠1=∠2（已知）
    ∴∠1=∠（    ）（等量代换）
    ∴EF∥CD（    ）
    ∴∠AEF=∠（    ）（    ）
    ∵EF⊥AB（已知）
    ∴∠AEF=90°（    ）
    ∴∠ADC=90°（    ）
    ∴CD⊥AB（    ）

    解：同位角相等，两直线平行；∠ACD；两直线平行，内错角相等；ACD；同位角相等，两直线平行；ADC；两直线平行，同位角相等；垂直定义；等量代换；垂直定义。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省姜堰市2012届九年级上学期期中考试数学试题 题型：044

    如图，已知正方形ABCD，将一个45度角∝的顶点放在D点并绕D点旋转，角的两边分别交AB边和BC边于点E和F，连接EF．求证：EF＝AE＋CF

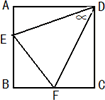
    (1)小明是这样思考的：延长BC到G，使得CG＝AE，连接DG，先证△DAE≌△DCG，再证△DEF≌△DGF，请你借助下图，按照小明的思路，写出完整的证明思路．

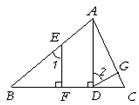
    (2)刘老师看到这条题目后，问了小明两个小问题：①如果正方形的边长和△BEF的面积都等于6，求EF的长②将角∝绕D点继续旋转，使得角∝的两边分别和AB边延长线、BC边的延长线交于E和F，如图所示，猜想EF、AE、CF三线段之间的数量关系并给予证明．请你帮忙解决．

    查看答案和解析>>

    科目：初中数学 来源：非常讲解·教材全解全析　数学　九年级下　（配北师大课标） 配北师大课标 题型：044

    已知二次函数y＝mx2＋3(m－)x＋4(m＜0)，与x轴交于A，B两点(A在B的左边)，与y轴交于点C，并且∠ACB＝90°，如下图所示，

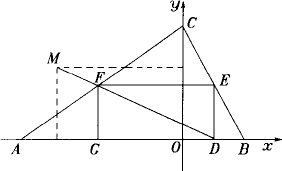
    (1)求这个二次函数的解析式；

    (2)矩形DEFG的一条边DG在AB上，E，F分别在BC，AC上，设OD＝x(x＞0)，矩形DEFG的面积为S，求S与x的函数关系式；

    (3)当矩形DEFG的面积S最大时，连结对角线DF并延长到M，使FM＝DF，试判断此时点M是否在二次函数y＝mx2＋3(m－)x＋4的图象上？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：学习周报　数学　沪科九年级版　2009－2010学年　第14期　总第170期 沪科版 题型：044

    已知正方形ABCD和正方形AEFG有一个公共点A，点G、E分别在线段AD、AB上．

    (1)如下图，连接DF、BF．若将正方形AEFG绕点A按顺时针方向旋转，请你判断命题“在旋转的过程中线段DF与BF的长度始终相等”是否正确，若正确，请说明理由；若不正确，请举反例说明；

    (2)若将正方形AEFG绕点A按顺时针方向旋转，连接DG，如下图．在旋转的过程中，你能否找到一条线段与线段DG的长度始终相等？并说明理由

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：解答题

    如下图，已知AD⊥BC，EF⊥BC，∠1=∠2，求证：DG∥BA
    证明：∵AD⊥BC，EF⊥BC （                ）
    ∴∠EFB=∠ADB=90°（               ）
    ∴EF∥AD（                ）
    ∴∠1=∠BAD（                    ）
    又∵∠1=∠2 （                     ）
    ∴_________（                   ）
    ∴DG∥BA（                 ）。

    查看答案和解析>>

    同步练习册答案