
(本小题满分8分)如下图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
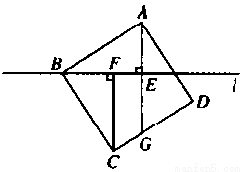
(1)求证:△ABE≌△ABE;
(2)若∠CBF=65°,求∠AGC的度数.
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源:2014-2015学年山东省九年级一模数学试卷(解析版) 题型:解答题
(12分)设抛物线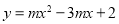 (
(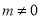 )与x轴的交点为A(
)与x轴的交点为A(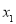 , 0),B(
, 0),B( ,0),且
,0),且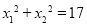 ,其中
,其中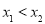 ,点P(a,b)为抛物线上一动点.
,点P(a,b)为抛物线上一动点.
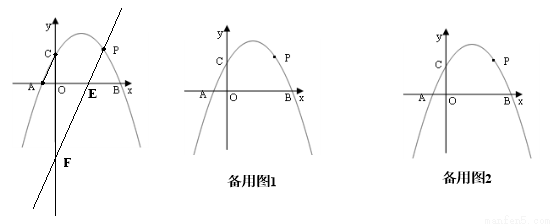
(1)求抛物线的解析式;
(2)连接AC,过P点做直线PE∥AC交x轴于点E,交y轴于点E(O,t),当a取何值时t有最大值,最大值是多少?
(3)判断在(2)的条件中是否存在一点P,使以点A、C、P、E为顶点的四边形为平行四边形.若不存在试说明理由;若存在,试求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级一模数学试卷(解析版) 题型:选择题
如图,在ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )

A.3:2 B.3:1 C.1:1 D.1:2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级中考第四次模拟数学试卷(解析版) 题型:解答题
(本小题满分14分)如下图,点A是抛物线C1: 的顶点,点B是抛物线C2:
的顶点,点B是抛物线C2: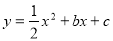 的顶点,并且OB⊥OA.
的顶点,并且OB⊥OA.

(1)求点A的坐标;
(2)若OB= ,求抛物线C2的函数解析式;
,求抛物线C2的函数解析式;
(3)在(2)条件下,设P为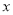 轴上的一个动点,探究:在抛物线C1或C2上是否存在点Q,使以点O,B,P,Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
轴上的一个动点,探究:在抛物线C1或C2上是否存在点Q,使以点O,B,P,Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级中考第四次模拟数学试卷(解析版) 题型:选择题
如下图,有四张不透明的卡片除正面的算式不同外,其余完全相同,将它们背面朝上洗匀后,从中随机抽取一张,则抽到的卡片上算式正确的概率是( )

A. B.
B.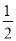 C.
C.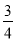 D.1
D.1
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(四川凉山卷)数学(解析版) 题型:解答题
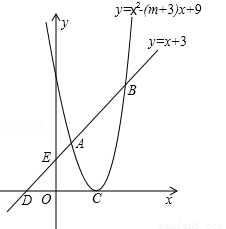
如图,已知抛物线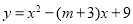 的顶点C在x轴正半轴上,一次函数
的顶点C在x轴正半轴上,一次函数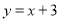 与抛物线交于A、B两点,与x、y轴交于D、E两点.
与抛物线交于A、B两点,与x、y轴交于D、E两点.
(1)求m的值.
(2)求A、B两点的坐标.
(3)点P(a,b)(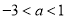 )是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.
)是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com