
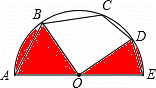
如图,AE是半圆O的直径,弦AB=BC=4![]() ,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为 .
,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为 .
考点:
扇形面积的计算;勾股定理;垂径定理;圆心角、弧、弦的关系.
专题:
综合题.
分析:
根据弦AB=BC,弦CD=DE,可得∠BOD=90°,∠BOD=90°,过点O作OF⊥BC于点F,OG⊥CD于点G,在四边形OFCG中可得∠FCD=135°,过点C作CN∥OF,交OG于点N,判断△CNG、△OMN为等腰直角三角形,分别求出NG、ON,继而得出OG,在Rt△OGD中求出OD,即得圆O的半径,代入扇形面积公式求解即可.
解答:
解:
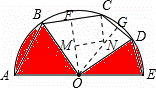
∵弦AB=BC,弦CD=DE,
∴点B是弧AC的中点,点D是弧CE的中点,
∴∠BOD=90°,
过点O作OF⊥BC于点F,OG⊥CD于点G,
则BF=FG=2![]() ,CG=GD=2,∠FOG=45°,
,CG=GD=2,∠FOG=45°,
在四边形OFCG中,∠FCD=135°,
过点C作CN∥OF,交OG于点N,
则∠FCN=90°,∠NCG=135°﹣90°=45°,
∴△CNG为等腰三角形,
∴CG=NG=2,
过点N作NM⊥OF于点M,则MN=FC=2![]() ,
,
在等腰三角形MNO中,NO=![]() MN=4,
MN=4,
∴OG=ON+NG=6,
在Rt△OGD中,OD=![]() =
=![]() =2
=2![]() ,
,
即圆O的半径为2![]() ,
,
故S阴影=S扇形OBD=![]() =10π.
=10π.
故答案为:10π.
点评:
本题考查了扇形的面积计算、勾股定理、垂径定理及圆心角、弧之间的关系,综合考察的知识点较多,解答本题的关键是求出圆0的半径,此题难度较大.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源:2013年初中毕业升学考试(浙江宁波卷)数学(解析版) 题型:填空题
如图,AE是半圆O的直径,弦AB=BC=4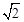 ,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为
.
,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为
.

查看答案和解析>>
科目:初中数学 来源:2013年浙江省宁波市中考数学试卷(解析版) 题型:填空题
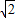 ,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为 .
,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为 .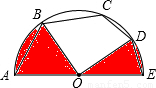
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com