
已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
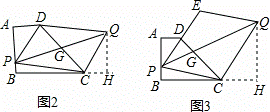
(1)如图1,P为AB边上的一点,以PD、PC为边作□PCQD,请问对角线PQ,DC的长能否相等,为什么?
(2)如图2,若P为AB边上一点,以PD,PC为边作□PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
(3)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE、PC为边作□PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
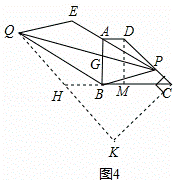
(4)如图3,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作□PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.

考点:
相似三角形的判定与性质;根的判别式;全等三角形的判定与性质;勾股定理;平行四边形的判定与性质。
专题:
代数几何综合题。
分析:
问题1:四边形PCQD是平行四边形,若对角线PQ、DC相等,则四边形PCQD是矩形,然后利用矩形的性质,设PB=x,可得方程x2+32+(2-x)2+1=8,由判别式△<0,可知此方程无实数根,即对角线PQ,DC的长不可能相等;
问题2:在平行四边形PCQD中,设对角线PQ与DC相交于点G,可得G是DC的中点,过点Q作QH⊥BC,交BC的延长线于H,易证得Rt△ADP≌Rt△HCQ,即可求得BH=4,则可得当PQ⊥AB时,PQ的长最小,即为4;
问题3:设PQ与DC相交于点G,PE∥CQ,PD=DE,可得![]() =
=![]() =
=![]() ,易证得Rt△ADP∽Rt△HCQ,继而求得BH的长,即可求得答案;
,易证得Rt△ADP∽Rt△HCQ,继而求得BH的长,即可求得答案;
问题4:作QH∥PE,交CB的延长线于H,过点C作CK⊥CD,交QH的延长线于K,易证得![]() =
=![]() 与△ADP∽△BHQ,又由∠DCB=45°,可得△CKH是等腰直角三角形,继而可求得CK的值,即可求得答案.
与△ADP∽△BHQ,又由∠DCB=45°,可得△CKH是等腰直角三角形,继而可求得CK的值,即可求得答案.
解答:
解:问题1:∵四边形PCQD是平行四边形,
若对角线PQ、DC相等,则四边形PCQD是矩形,
∴∠DPC=90°,
∵AD=1,AB=2,BC=3,
∴DC=2![]() ,
,
设PB=x,则AP=2-x,
在Rt△DPC中,PD2+PC2=DC2,即x2+32+(2-x)2+1=8,
化简得x2-2x+3=0,
∵△=(-2)2-4×1×3=-8<0,
∴方程无解,
∴对角线PQ与DC不可能相等.
问题2:如图2,在平行四边形PCQD中,设对角线PQ与DC相交于点G,
则G是DC的中点,
过点Q作QH⊥BC,交BC的延长线于H,
∵AD∥BC,
∴∠ADC=∠DCH,即∠ADP+∠PDG=∠DCQ+∠QCH,
∵PD∥CQ,
∴∠PDC=∠DCQ,
∴∠ADP=∠QCH,
又∵PD=CQ,
∴Rt△ADP≌Rt△HCQ,
∴AD=HC,
∵AD=1,BC=3,
∴BH=4,
∴当PQ⊥AB时,PQ的长最小,即为4.
问题3:如图3,设PQ与DC相交于点G,
∵PE∥CQ,PD=DE,
∴![]() =
=![]() =
=![]() ,
,
∴G是DC上一定点,
作QH⊥BC,交BC的延长线于H,
同理可证∠ADP=∠QCH,
∴Rt△ADP∽Rt△HCQ,
即![]() =
=![]() =
=![]() ,
,
∴CH=2,
∴BH=BG+CH=3+2=5,
∴当PQ⊥AB时,PQ的长最小,即为5.
问题4:如图3,设PQ与AB相交于点G,
∵PE∥BQ,AE=nPA,
∴![]() =
=![]() ,
,
∴G是DC上一定点,
作QH∥PE,交CB的延长线于H,过点C作CK⊥CD,交QH的延长线于K,
∵AD∥BC,AB⊥BC,
∴∠D=∠QHC,∠DAP+∠PAG=∠QBH+∠QBG=90°,∠PAG=∠QBG,
∴∠QBH=∠PAD,
∴△ADP∽△BHQ,
∴![]() ,
,
∵AD=1,
∴BH=n+1,
∴CH=BH+BC=3+n+1=n+4,
过点D作DM⊥BC于M,
则四边形ABND是矩形,
∴BM=AD=1,DM=AB=2
∴CM=BC-BM=3-1=2=DM,
∴∠DCM=45°,
∴∠KCH=45°,
∴CK=CH•cos45°=![]() (n+4),
(n+4),
∴当PQ⊥CD时,PQ的长最小,最小值为![]() (n+4).
(n+4).
点评:
此题考查了相似三角形的判定与性质、直角梯形的性质、平行四边形的性质、矩形的性质、勾股定理、一元二次方程根的判别式、全等三角形的判定与性质以及直角三角形的性质等知识.此题难度较大,注意准确作出辅助线是解此题的关键,注意数形结合思想与方程思想的应用.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
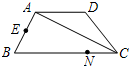 如图,已知梯形ABCD,AD∥BC,AD=DC=4,BC=8,点N在BC上,CN=2,E是AB中点,在AC上找一点M使EM+MN的值最小,此时其最小值一定等于( )
如图,已知梯形ABCD,AD∥BC,AD=DC=4,BC=8,点N在BC上,CN=2,E是AB中点,在AC上找一点M使EM+MN的值最小,此时其最小值一定等于( )| A、6 | ||
| B、8 | ||
| C、4 | ||
D、4
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.
如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:
 秒2
秒2| 3 |
| 29 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com