
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
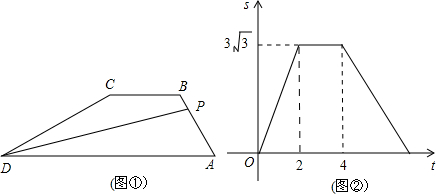
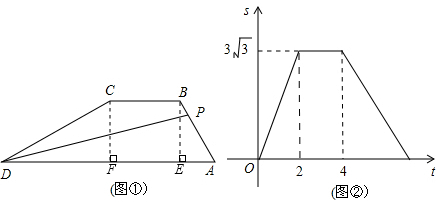 解:由图②可知,t在2到4秒时,△PAD的面积不发生变化,
解:由图②可知,t在2到4秒时,△PAD的面积不发生变化,| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| CF2+DF2 |
| 3+9 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| CF |
| DF |
| ||
| 6-1-2 |
| ||
| 3 |


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
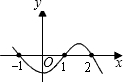 已知y是关于x的函数,函数图象如图,则当y>0时,自变量x的取值范围是( )
已知y是关于x的函数,函数图象如图,则当y>0时,自变量x的取值范围是( )| A、x<0 |
| B、-1<x<1或x>2 |
| C、x>-1 |
| D、x<-1或1<x<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
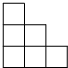 一些完全相同的小正方体搭成一个几何体,这个几何体从正面和左面看所得的平面图形均为如图,小正方体的块数最多有( )
一些完全相同的小正方体搭成一个几何体,这个几何体从正面和左面看所得的平面图形均为如图,小正方体的块数最多有( )| A、11块 | B、12块 |
| C、13块 | D、14块 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、0.69×106 |
| B、6.82×1 05 |
| C、0.68×106 |
| D、6.8×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、y=0.2+0.1x |
| B、y=0.1x |
| C、y=-0.1+0.1x |
| D、y=0.5+0.1x |
查看答案和解析>>
科目:初中数学 来源: 题型:
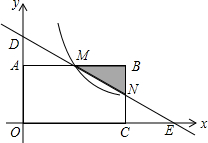 如图在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
如图在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| AN+OM |
| O′O″ |
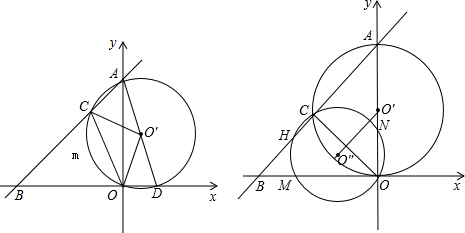
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com