
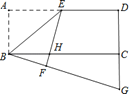
【题目】已知如图,在长方形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则AB=________.
【答案】9
【解析】
连结GE,根据折叠的性质和矩形的性质可得△EFG与△EDG是直角三角形,DE=AE=FE,再根据HL即可证明△EFG≌△EDG.根据全等三角形的性质可得DG=FG=16,可设AB=BF=DC=x,求出x即可.
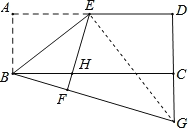 连结GE.
连结GE.
∵E是边AD的中点,
∴DE=AE=FE,
又∵四边形ABCD是矩形,
∴∠D=∠A=∠BFE=90°,
∴∠D=∠EFG=90°
在Rt△EFG与Rt△EDG中,
EF=ED,EG=EG,
∴Rt△EFG≌Rt△EDG(HL);
∴DG=FG=16,
设DC=x,则CG=16x,BG=x+16
在Rt△BCG中,
BG2=BC2+CG2,
即(x+16)2=(16x)2+242,
解得x=9,∴AB=9.
故答案为9.


科目:初中数学 来源: 题型:
【题目】某校为了了解学生在校吃午餐所需时间的情况,抽查了20名同学在校吃午餐所花的时间,获得如下数据(单位:min):
10,12,15,10,16,18,19,18,20,38,
22,25,20,18,18,20,15,16,21,16.
(1)若将这些数据分为6组,请列出频数表,画出频数直方图;
(2)根据频数直方图,你认为校方安排学生吃午餐时间多长为宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E. 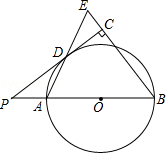
(1)求证:AB=BE;
(2)若PA=2,cosB= ![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
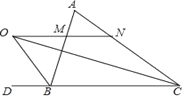
【题目】如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.
求证:(1)MO=MB;(2)MN=CN﹣BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
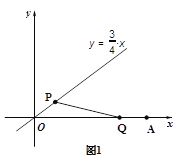
【题目】已知在平面直角坐标系中,A(9,0),直线l:y=![]() .P,Q两点分别同时从O,A出发,P点沿直线l向上运动,Q点沿x轴向左运动,它们的速度相同.连接PQ,当
.P,Q两点分别同时从O,A出发,P点沿直线l向上运动,Q点沿x轴向左运动,它们的速度相同.连接PQ,当
PQ⊥x轴时,P,Q两点同时停止运动.设P点的横坐标为m(m≥0),
(1)求m的取值范围;
(2)如图1,当△OPQ是以OP为腰的等腰三角形时,求m的值;
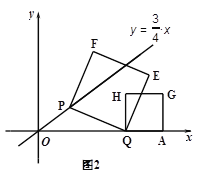
(3)如果以PQ为边在上方作正方形PQEF,以AQ为边在上方作正方形 QAGH,如图2,
①用含m的代数式表示E点的坐标;
②当正方形PQEF的某个顶点(Q点除外)落在正方形 QAGH的边上,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOC与∠BOD都是直角,∠BOC=65°
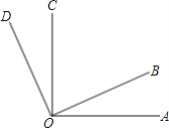
(1)求∠AOD的度数;
(2)∠AOB与∠DOC有何大小关系?
(3)若不知道∠BOC的具体度数,其他条件不变,(2)的关系仍成立吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
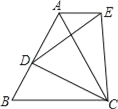
【题目】如图,等边△ABC中,D是AB边上的一动点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:△ACE≌△BCD;
(2)判断AE与BC的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com