
 已知,某一次函数与反比例函数相交于A(1,3),B(m,1),求:
已知,某一次函数与反比例函数相交于A(1,3),B(m,1),求:分析 (1)设一次函数与反比例函数的解析式分别为y=ax+b(k≠0),y=$\frac{k}{m}$(k≠0),将A坐标代入反比例解析式中求出k的值,确定出反比例解析式,再将B坐标代入反比例解析式中求出m的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出a与b的值,即可确定出一次函数解析式;
(2)设一次函数与x轴交于C点,求出C坐标,三角形AOB的面积=三角形AOC-三角形BOC的面积,求出即可.
解答 解:(1)设一次函数与反比例函数的解析式分别为y=ax+b(k≠0),y=$\frac{k}{m}$(k≠0),
∵反比例函数y=$\frac{k}{m}$(k≠0)的图象经过点A(1,3),
∴k=1×3=3,
∴反比例函数的解析式为y=$\frac{3}{x}$,
∵点B(m,1)在反比例函数的图象上,
∴1=$\frac{3}{m}$
∴m=3,
∴点B的坐标为(3,1),
∵一次函数的图象经过点A,B,
将这两个点的坐标代入y=kx+b,得$\left\{\begin{array}{l}{3=a+b}\\{1=3a+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=4}\end{array}\right.$,
则所求一次函数的解析式为y=-x+4;
(2)设一次函数y=-x+4的图象交x轴于点C,
∴C点坐标为(4,0),即OC=4,
∵A点的纵坐标为3,B点的纵坐标为1,
∴S△AOB=S△AOC-S△BOC=$\frac{1}{2}$OC•3-$\frac{1}{2}$OC•1=$\frac{1}{2}$×4×2=4.
点评 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法确定函数解析式,一次函数与x轴的交点,坐标与图形性质,以及三角形的面积求法,熟练掌握待定系数法是解本题的关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,在这个漂亮的螺旋图中,所有的三角形都是直角三角形,按此方式继续画下去:根据图中所标数据.
如图,在这个漂亮的螺旋图中,所有的三角形都是直角三角形,按此方式继续画下去:根据图中所标数据.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.94×103 | B. | 3.94×104 | C. | 39.4×103 | D. | 0.394×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$a元 | B. | $\frac{10}{9}$a元 | C. | $\frac{1}{10}$a元 | D. | 10a元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校八年级以“我最喜爱的体育运动”为主题对该校八年级每位学生进行了调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),经调查每位同学都做了选择,根据调查结果绘制如下统计图表:
某校八年级以“我最喜爱的体育运动”为主题对该校八年级每位学生进行了调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),经调查每位同学都做了选择,根据调查结果绘制如下统计图表:| 运动项目 | 频数 |
| 篮球 | 90 |
| 羽毛球 | m |
| 乒乓球 | 108 |
| 跳绳 | 54 |
| 其它 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
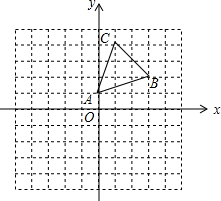 如图,△ABC的顶点均在正方形网格的格点上,在已知的直角坐标系中,A(0,1),B(3,2).
如图,△ABC的顶点均在正方形网格的格点上,在已知的直角坐标系中,A(0,1),B(3,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 由一些大小相同的小正方形组成的几何体俯视图和左视图如图所示,那么,组成这个几何体的小正方体个数可能有( )
由一些大小相同的小正方形组成的几何体俯视图和左视图如图所示,那么,组成这个几何体的小正方体个数可能有( )| A. | 8块 | B. | 6块 | C. | 4块 | D. | 12块 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com