
【题目】如图,某汽车在路面上朝正东方向匀速行驶,在A处观测到楼H在北偏东60°方向上,行驶1小时后到达B处,此时观测到楼H在北偏东30°方向上,那么该车继续行驶( )分钟可使汽车到达离楼H距离最近的位置.
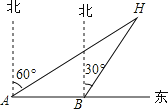
A.60 B.30 C.15 D.45
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
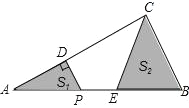
A. 一直减小B. 一直不变C. 先减小后增大D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.

(1)请画出这个几何体的俯视图;
(2)图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOBC的顶点O在原点,边AO,BO分别在x轴和y轴上,点C坐标为(4,4),点D是BO的中点,点P是边OA上的一个动点,连接PD,以P为圆心,PD为半径作圆,设点P横坐标为t,当⊙P与正方形AOBC的边相切时,t的值为_____.
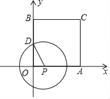
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,CD⊥AB于点D,点O是∠BAC的平分线上一点,⊙O与AB相切于点M,与CD相切于点N
(1)求证:∠AOC=135°;
(2)若NC=3,BC=2![]() ,求DM的长.
,求DM的长.
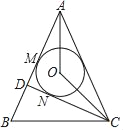
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
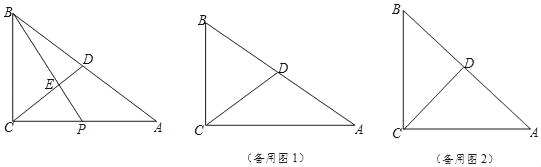
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;
(2)联结PD,如果PD⊥AB,且CE=2,ED=3,求cosA的值;
(3)联结PD,如果BP2=2CD2,且CE=2,ED=3,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:sin30°=![]() ,tan30°=
,tan30°=![]() ,sin45°=
,sin45°=![]() ,tan45°=1,sin60°=
,tan45°=1,sin60°=![]() ,tan60°=
,tan60°=![]() ,由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
,由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
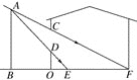
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=120°,点A,B分別在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°,且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD.
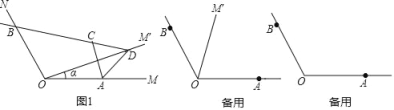
(1)求证:AD=CD;
(2)如图1,当0°<α<60°时,试证明∠ACD的大小是一个定值;
(3)当60°<α<120°时,(2)中的结论还成立吗?请补全图形并说明理由;
(4)△ACD面积的最大值为 .(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com