
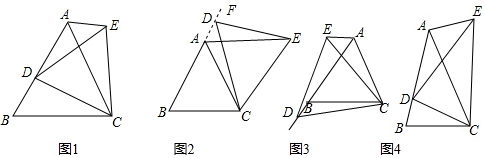
分析 (1)①根据等边三角形的性质得到AB=AC,CD=CE,∠ACB=∠DCE=60°,利用SAS可证明△BCD≌△ACE,继而得出结论;
②同①的方法判断出△BCD≌△ACE即可;
③同①的方法判断出△BCD≌△ACE即可;
(2)首先得出∠ACB=∠ECD,从而判定△ABC∽△EDC,得到$\frac{AC}{CE}=\frac{BC}{CD}$,根据∠BCD=∠ACB-∠ACD,∠ACE=∠DCE-∠ACD,于是得到∠BCD=∠ACE,推出△BCD∽△ACE,即可得出结论
解答 (1)①证明:∵△ABC、△CDE是等边三角形,
∴AB=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE,
∵在△BCD和△ACE中,$\left\{\begin{array}{l}{AC=BC}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$
∴△BCD≌△ACE(SAS),
∴∠ABC=∠EAC;
故答案为:∠ABC=∠EAC;
②解:结论∠ABC=∠EAC仍成立;
理由如下:∵△ABC、△CDE是等边三角形,
∴AB=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,$\left\{\begin{array}{l}{AB=AC}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$
∴△BCD≌△ACE(SAS),
∴∠ABC=∠EAC;
③∵△ABC、△CDE是等边三角形,
∴∠ACB=∠DCE=∠ABC=60°,
∴∠ACE=∠BCD,
在△BCD和△ACE中,$\left\{\begin{array}{l}{AB=AC}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$
∴△BCD≌△ACE(SAS),
∴∠DBC=∠EAC,
∵∠ABC+∠DBC=180°,
∴∠ABC+∠EAC=180°,
∵∠ABC=60°,
∴∠EAC=120°=2∠ABC.
故答案为:∠ABC+∠EAC=180°或∠EAC=2∠ABC
(2)解:∠ABC=∠EAC;
理由如下:∵AB=AC,ED=EC,顶角∠BAC=∠DEC,
∴底角∠ACB=∠ECD,
∴△ABC∽△EDC,
∴$\frac{AC}{CE}=\frac{BC}{CD}$,
又∵∠BCD=∠ACB-∠ACD,∠ACE=∠DCE-∠ACD,
∴∠BCD=∠ACE,
∴△BCD∽△ACE,
∴∠ABC=∠CAE.
点评 此题是三角形综合题,主要考查了等边三角形的性质,等腰三角形的性质,相似三角形的判定与性质、全等三角形的判定与性质,解答本题的关键是仔细观察图形,找到全等(相似)的条件,利用全等(相似)的性质证明结论.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中(AB≠BC),直 线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
如图,在平行四边形ABCD中(AB≠BC),直 线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5000(1+x)+5000(1+x)2=7200 | B. | 5000(1+x2)=7200 | ||
| C. | 5000(1+x)2=7200 | D. | 5000+5000(1+x)2=7200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
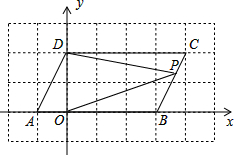 在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b-2|+$\sqrt{2a-b+5}$=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.
在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b-2|+$\sqrt{2a-b+5}$=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com