
 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得10元的购物券.
某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得10元的购物券.分析 (1)找到红色、黄色或绿色区域的份数之和占总份数的多少即为获得购物券的概率.
(2)应计算出转转盘所获得的购物券与直接获得10元的购物券相比较便可解答.
解答 解:(1)整个圆周被分成了20份,转动一次转盘获得购物券的有9种情况,
所以转动一次转盘获得购物券的概率=$\frac{9}{20}$;
(2)根据题意得:转转盘所获得的购物券为:50×$\frac{1}{20}$+30×$\frac{3}{20}$+20×$\frac{5}{20}$=11.5(元),
∵11.5元>10元,
∴选择转盘对顾客更合算.
点评 本题考查了概率公式的运用,易错点在于准确无误的找到红色、黄色或绿色区域的份数之和,关键是理解获胜的概率即为可能获胜的份数之和与总份数的比.


科目:初中数学 来源: 题型:解答题
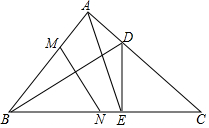 如图,△ABC中,∠BAC=90°,AB=AC,D为AC上一点,DE⊥BC于E,连接BD,M在AB上,AM=AD,MN⊥BD交BC于点N,若MN=5,AE=5$\sqrt{2}$,求BC的长.
如图,△ABC中,∠BAC=90°,AB=AC,D为AC上一点,DE⊥BC于E,连接BD,M在AB上,AM=AD,MN⊥BD交BC于点N,若MN=5,AE=5$\sqrt{2}$,求BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图.在正方形ABCD中,点P是BC延长线上一点,BQ⊥PD于点Q,QN⊥BD于点N,连接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,则AN的长为$\sqrt{10}$.
如图.在正方形ABCD中,点P是BC延长线上一点,BQ⊥PD于点Q,QN⊥BD于点N,连接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,则AN的长为$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
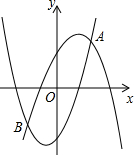 如图,抛物线y1=a(x+1)2-5与抛物线y2=-a(x-1)2+5(a≠0)的交点A,B,点A,B的坐标分别是(2,4),(m,-4),若无论x取何值,y总取y1,y2中的最小值.则y的最大值是( )
如图,抛物线y1=a(x+1)2-5与抛物线y2=-a(x-1)2+5(a≠0)的交点A,B,点A,B的坐标分别是(2,4),(m,-4),若无论x取何值,y总取y1,y2中的最小值.则y的最大值是( )| A. | 5 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com