Question

①如图1，AB∥CD，则∠A+∠E+∠C=180°；②如图2，AB∥CD，则∠E=∠A+∠C；③如图3，AB∥CD，则∠A+∠E-∠1=180°；④如图4，AB∥CD，则∠A=∠C+∠P．以上结论正确的个数是

1. A.
   1个
2. B.
   2个
3. C.
   3个
4. D.
   4个

Answer 1

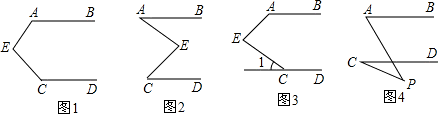
B
分析：①过点E作直线EF∥AB，由平行线的性质即可得出结论；
②过点E作直线EF∥AB，由平行线的性质即可得出结论；
③过点E作直线EF∥AB，由平行线的性质可得出∠A+∠E-∠1=180°；
④先根据三角形外角的性质得出∠1=∠C+∠P，再根据∠A+∠1=1180°即可作出判断．
解答：①过点E作直线EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠A+∠1=180°，∠2+∠C=180°，
∴∠A+∠B+∠E=360°，故本选项错误；
②过点E作直线EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠A=∠1，∠2=∠C，
∴∠AEC=∠A+∠C，即∠E=∠A+∠C，故本选项正确；
③过点E作直线EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠A+∠3=180°，∠1=∠2，
∴∠A+∠AEC-∠1=180°，即∠A+∠E-∠1=180°，故本选项正确；
④∵∠1是△CEP的外角，
∴∠1=∠C+∠P，
∵AB∥CD，
∴∠A+∠1=180°，即∠A=180°-∠A-∠P，故本选项错误．

故选B．
点评：本题考查的是平行线的性质及三角形外角的性质，根据题意作出辅助线是解答此题的关键．