
【题目】已知:点O到△ABC的两边AB、AC所在直线的距离OD=OE,且OB=OC.
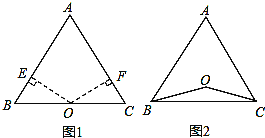
(1)如图,若点O在BC上,求证:AB=AC;
(2)如图,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.


【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)求证AB=AC,就是求证∠B=∠C,可通过构建全等三角形来求.过点O分别作OE⊥AB于E,OF⊥AC于F,那么可以用斜边直角边定理(HL)证明Rt△OEB≌Rt△OFC来实现;(2)首先得出Rt△OEB≌Rt△OFC,进而得出AB=AC;(3)不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC.
试题解析:(1)证明:过点O分别作OE⊥AB于E,OF⊥AC于F,
由题意知,
在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:过点O分别作OE⊥AB于E,OF⊥AC于F,
由题意知,OE=OF.∠BEO=∠CFO=90°,
∵在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠OBE=∠OCF,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
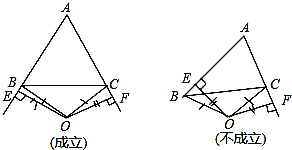
(3)不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC,否则AB≠AC.(如图)


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:

(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)请你设计一种方案,不仅每小时支付的租金最少,又恰好能完成每小时的挖掘量?
查看答案和解析>>
科目:初中数学 来源: 题型:
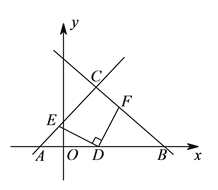
【题目】如图,在平面直角坐标系中,已知直线![]() 和
和![]() 与
与![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,设两直线相交于点
,设两直线相交于点![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上一个动点(不与点
上一个动点(不与点![]() 和
和![]() 重合),连结
重合),连结![]() ,并过点
,并过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(![]() )判断
)判断![]() 的形状,并说明理由.
的形状,并说明理由.
(![]() )当点
)当点![]() 在线段
在线段![]() 上运动时,四边形
上运动时,四边形![]() 的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.
(![]() )当点
)当点![]() 的横坐标为
的横坐标为![]() 时,在
时,在![]() 轴上找到一点
轴上找到一点![]() 使得
使得![]() 的周长最小,请直接写出点
的周长最小,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为________;
(2)该同学从5个项目中任选两个,利用树状图或列表列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
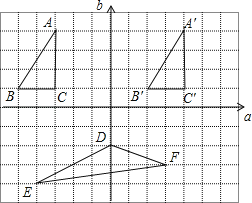
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点△A′B′C′是由格点△ABC通过怎样的变换得到的?
(2)如果以直线a、b为坐标轴建立平面直角坐标系后,点A的坐标为(﹣3,4),请写出格点△DEF各顶点的坐标,并求出△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过P(-2·3).
(1)求此反比例函数的解析式;
(2)点A(2.-3)、B(3,2)是否在这个函数的图象上?
(3)这个函数的图象位于哪些象限?函数值y随自变量x的减小如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(![]() )求抛物线的解析式.
)求抛物线的解析式.
(![]() )设抛物线的顶点为
)设抛物线的顶点为![]() ,点
,点![]() 在抛物线的对称轴上,且
在抛物线的对称轴上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(![]() )点
)点![]() 在直线
在直线![]() 上方的抛物线上,是否存在点
上方的抛物线上,是否存在点![]() 使
使![]() 的面积最大,若存在,请求出点
的面积最大,若存在,请求出点![]() 坐标.
坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com