
分析 设则$\frac{{x}^{2}+2}{x}$=y,原方程化为y-$\frac{3}{y}$=2,进而化为整式方程即可求得结论.
解答 解:设则$\frac{{x}^{2}+2}{x}$=y,
原方程化为y-$\frac{3}{y}$=2,
∴y2-2y-3=0,
解得:y1=3,y2=-1,
当y1=3时,$\frac{{x}^{2}+2}{x}$=3,
∴x2-3x+2=0,
∵△=1>0,
∴y1=3符合题意,当y2=-1,$\frac{{x}^{2}+2}{x}$=-1,
∴x2,+x+2=0,
∵△=-71<0,
∴y2=-1不符合题意,
故答案为3.
点评 本题主要考查了换元法解方程,分式方程的解法,能正确设出未知数是解题的关键,同时注意还原为x的方程时,要判别是否有实根.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
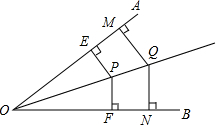 如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.
如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com