练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

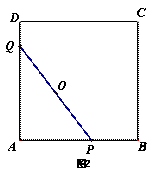
    如图1，折线段AOB将面积为S的⊙O分成两个扇形，大扇形、小扇形的面积分别为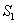、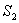，若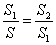=0.618，则称分成的小扇形为“黄金扇形”，生活中的折扇（如图2），大致是“黄金扇形”，则“黄金扇形”的圆心角约为          °.(精确到0.1)


    137.5

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，两个大小不同的实心球在水平面靠在一起组成如图所示的几何体，则该几何体的左视图是（　　）

    　   A．两个外切的圆  B．                             两个内切的圆             C． 两个内含的圆  D． 一个圆

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若不等式组有解，则实数a的取值范围是（　　）

    　  A．a＜﹣36      B． a≤﹣36         C． a＞﹣36         D． a≥﹣36

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系中，点P（-2，3）关于原点对称的点Q的坐标为

    A．（2，-3） B．（2，3）  C．（3，-2） D．（-2，-3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算=                 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    我市启动了第二届“美丽港城·美在悦读”全民阅读活动。为了了解市民每天的阅读时间情况，随机抽取了部分民进行调查。根据调查结果绘制如下尚不完整的频数分布表：

    阅读时间

    x（min）

    0≤x<30

    30≤x<60

    60≤x<90

    x<≥90

    合计

    频数

    450

    400

    50

     

    频率

    0．4

    0．1

    1

        （1）补全表格：

    （2）将每天阅读时间不低于60min的市民称为“阅读爱好者”。若我市约有500万人，请估计我市能称为“阅读爱好者”的市民有多少万人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某数学兴趣小组对线段上的动点问题进行探究，已知AB=8.

    问题思考：

    如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC与正方形PBFE.

    （1）在点P运动时，这两个正方形面积之和是定值吗？如果时求出；若不是，求出这两个正方形面积之和的最小值.

    （2）分别连接AD、DF、AF，AF交DP于点A，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由.

    问题拓展：

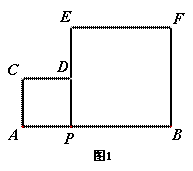
    （3）如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8.若点P从点A出发，沿A→B→C→D的线路，向D点运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长。

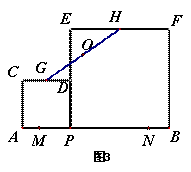
     (4)如图（3），在“问题思考”中，若点M、N是线段AB上的两点，且AM=BM=1，点G、H分别是边CD、EF的中点.请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+OB的最小值.

        

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，矩形中，，,点是边上一点，把沿折叠，使点落在点处，则①      ；②当△为直角三角形时，＝        ．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在Rt△ABC中，∠C=90°，若sinA=，则cosB的值是（　　）

    　   A．                    B．                                C．                           D．  

    查看答案和解析>>

    同步练习册答案