
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
分析 作出图形,根据三角形的中位线定理可得EF=GH=$\frac{1}{2}$AC,FG=EH=$\frac{1}{2}$BD,再根据矩形的对角线相等可得AC=BD,从而得到四边形EFGH的四条边都相等,然后根据四条边都相等的四边形是菱形解答.
解答  解:如图,连接AC、BD,
解:如图,连接AC、BD,
∵E、F、G、H分别是矩形ABCD的AB、BC、CD、AD边上的中点,
∴EF=GH=$\frac{1}{2}$AC,FG=EH=$\frac{1}{2}$BD(三角形的中位线等于第三边的一半),
∵矩形ABCD的对角线AC=BD,
∴EF=GH=FG=EH,
∴四边形EFGH是菱形.
故选B.
点评 本题考查了三角形的中位线定理,菱形的判定,矩形的性质,作辅助线构造出三角形,然后利用三角形的中位线定理是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x+y=100\\ 3x+3y=100\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=100\\ x+\frac{1}{3}y=100\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=100\\ 3x+\frac{1}{3}y=100\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=100\\ 3x+y=100\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
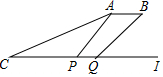 某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93,$\sqrt{3}$≈1.73)
某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④S△CEF=2S△ABE,其中正确的结论有( )
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④S△CEF=2S△ABE,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
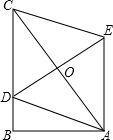 如图,在Rt△ABC中,∠B=90°,AB=3,∠BCA=30°,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE最小值是3.
如图,在Rt△ABC中,∠B=90°,AB=3,∠BCA=30°,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE最小值是3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.061994×105万元 | B. | 4.061994×106万元 | ||
| C. | 4.061994×104万元 | D. | 40.61994×103万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com