

���� ��1��ֱ�����ô���ϵ��������κ�������ʽ�ó����ɣ�
��2�����ȵó���GQM�ա�POM��ASA���������ó���G��������C1�ϣ��ó�2m2=$\frac{1}{9}$��-3-3��2�������ó��𰸣�
��3�����ú����Գ��Ա�ʾ��A�����꣬�ٱ�ʾ��MC��PQ�ij��������ó����ֵ��
��� ��1���⣺��������C1�Ľ���ʽ��y=a��x-3��2��a��0���������㣨0��1����
��1=a��0-3��2��
��ã�a=$\frac{1}{9}$��
��2���ٽ⣺��A��C�������y��Գƣ�
���MΪAC���е㣬
���ı���APCG��ƽ���ı��Σ�����е�M��PG���е㣬
����G��GQ��y���ڵ�Q��
�ڡ�GQM�͡�POM��
$\left\{\begin{array}{l}{��GQM=��POM}\\{QM=OM}\\{��QMG=��OMP}\end{array}\right.$��
���GQM�ա�POM��ASA����
��GQ=PO=3��MQ=OM=m2��OQ=2m2��
���G��-3��2m2����
�߶���G��������C1�ϣ�
��2m2=$\frac{1}{9}$��-3-3��2��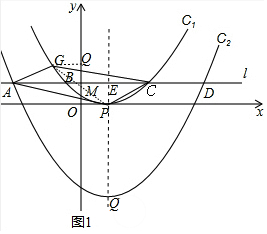
��ã�m=��$\sqrt{2}$��
�֡�m��0��
��m=$\sqrt{2}$��
�൱m=$\sqrt{2}$ʱ���ı���APCG��ƽ���ı��Σ�
��֤������������y=$\frac{1}{9}$��x-3��2�У���y=m2��
��ã�x=3��3m��
�֡�m��0���ҵ�C�ڵ�B���Ҳ࣬
��C��3+3m��m2����MC=3+3m��
��A��C�������y��Գƣ�
��A��-3-3m��m2����
�߽�������C1����ƽ��h��h��0������λ�õ�������C2��
��������C2�Ľ���ʽΪ��y=$\frac{1}{9}$��x-3��2-h��
��m2=$\frac{1}{9}$��-3-3m-3��2-h��
��ã�h=4m+4��
��PQ=4+4m��
��$\frac{MC}{PQ}$=$\frac{3+3m}{4+4m}$=$\frac{3}{4}$��
���� ���⿼����κ����ۺ��⡢ƽ�Ʊ任��ȫ�������ε��ж������ʡ�ƽ���ı��ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ò���������⣬�����п�ѹ���⣮


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
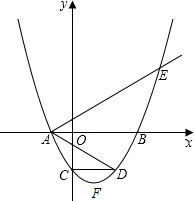 ��ͼ�����κ���y=a��x2-4mx-12m2��������a��m�dz�������a��0��m��0����ͼ����x��ֱ��ڵ�A��B����Aλ�ڵ�B����ࣩ����y�ύ��C��0��-6������D�ڶ��κ�����ͼ���ϣ�CD��AB������AD������A������AE�����κ�����ͼ���ڵ�E��ABƽ�֡�DAE��
��ͼ�����κ���y=a��x2-4mx-12m2��������a��m�dz�������a��0��m��0����ͼ����x��ֱ��ڵ�A��B����Aλ�ڵ�B����ࣩ����y�ύ��C��0��-6������D�ڶ��κ�����ͼ���ϣ�CD��AB������AD������A������AE�����κ�����ͼ���ڵ�E��ABƽ�֡�DAE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ�����ڸۿ�A������100 n mi1e��B��������Σ�պ���25 n mile/h���ٶ�������Ư���ҷ�������źţ�һ�����ӵ�����źź������ɸۿ�A��50 n mile/h���ٶ���ƫ�������У���ȥ֧Ԯ�����������$\frac{200\sqrt{3}}{3}$n mi1e���ϻ�����
��ͼ��һ�����ڸۿ�A������100 n mi1e��B��������Σ�պ���25 n mile/h���ٶ�������Ư���ҷ�������źţ�һ�����ӵ�����źź������ɸۿ�A��50 n mile/h���ٶ���ƫ�������У���ȥ֧Ԯ�����������$\frac{200\sqrt{3}}{3}$n mi1e���ϻ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
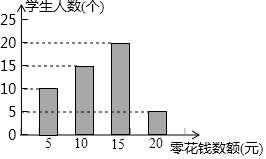 ij��ʦΪ�˶�ѧ���㻨Ǯ��ʹ�ý��н���ָ������ȫ��50��ѧ��ÿ��һ���ڵ��㻨Ǯ�������ͳ�Ƶ��飬��������ͳ�Ʊ���ͳ��ͼ����ͼ��ʾ��
ij��ʦΪ�˶�ѧ���㻨Ǯ��ʹ�ý��н���ָ������ȫ��50��ѧ��ÿ��һ���ڵ��㻨Ǯ�������ͳ�Ƶ��飬��������ͳ�Ʊ���ͳ��ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
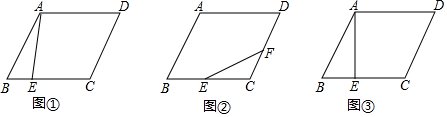
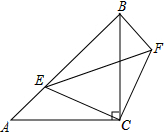 ��֪����ͼ����ABC�͡�EFC���ǵ���ֱ�������Σ���ACB=��ECF=90�㣬��E��AB���ϣ�
��֪����ͼ����ABC�͡�EFC���ǵ���ֱ�������Σ���ACB=��ECF=90�㣬��E��AB���ϣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com