
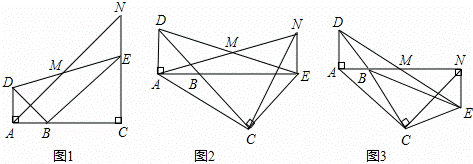
如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时, 当A,B,M,N在同一直线上时,
(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
 |
(1)如图1,证△ADM≌△NEM,可得AM=MN.( 4分 )
(2)如图2,先证△ADM≌△NEM,∴AD=NE .∴AB=NE.( 4分 )
.∴AB=NE.( 4分 )
再证△ABC≌△NEC,∴AC=NC,∠ACB=∠NCE.∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.
(3)△ACN仍为等腰直角 三角形.( 4分 )
三角形.( 4分 )
如图3,∵AD∥EN,∠DAB=90°,∴∠ENA=∠DAN=90°.
∵∠BCE=90°,∴∠CBN+∠CEN=360°﹣90°﹣90°=180°.
∵A、B、N三点在同一条直线上,∴∠ABC+∠CBN=180°.∴∠ABC=∠NEC .
.
∵△ADM≌△NEM(已证),∴AD=NE.
∵AD=AB,∴AB=NE.∴△ABC≌△NEC.∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.∴△ACN为等腰直角三角形.( 4分 )


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
问题情境:
如图1,P是⊙O外的一点,直线PO分别交⊙O于点A、B,则PA是点P到⊙O上的点的最短距离.
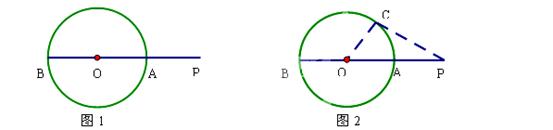
探究:
请您结合图2给予证明,
归纳:
圆外一点到圆上各点的最短距离是:这点到连接这点与圆心连线与圆交点之间的距离.
图中有圆,直接运用:
如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是 上的一个动点,连接AP,则AP的最小值是 .
上的一个动点,连接AP,则AP的最小值是 .

|
图中无圆,构造运用:
如图4,在边长为2的菱形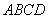 中,∠
中,∠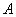 =60°,
=60°, 是
是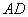 边的中点,
边的中点, 是
是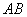 边上一动点,将△
边上一动点,将△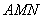 沿
沿 所在的直线翻折得到△
所在的直线翻折得到△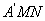 ,连接
,连接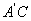 ,请求出
,请求出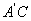 长度的最小
长度的最小
值.

 | |||
|
解:由折叠知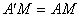 ,又M是AD的中点,可得
,又M是AD的中点,可得 ,故点
,故点 在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
迁移拓展,深化运用:
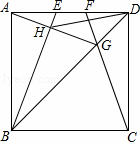
如图6,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
|
查看答案和解析>>
科目:初中数学 来源: 题型:
如图是两个全等的含30°角的直角三角形.
(1)将其相等边拼在一起,组成一个没有重叠部分的平面图形,请你画出所有不同的拼接平面图形的示意图;
(2)若将(1)中平面图形分别印制在质地、形状、大小完全相同的卡片上,洗匀后从中随机抽取一张,求抽取的卡片上平面图形为轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
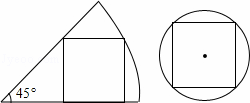
一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是--------( )
|
| A. | 5:4 | B. | 5:2 | C. |
| D. |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com