
【题目】我们知道,无限循环小数都可以转化为分数.例如:将 ![]() 转化为分数时,可设
转化为分数时,可设 ![]() =x,则x=0.3+
=x,则x=0.3+ ![]() x,解得x=
x,解得x= ![]() ,即
,即 ![]() =
= ![]() .仿此方法,将
.仿此方法,将 ![]() 化成分数是 .
化成分数是 .
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=x2+bx+c的顶点坐标为(﹣1,1),直线1的解析式为y2=2mx+3m2+4nm+4n2,且l与x轴、y轴分别交于A、B两点.
(1)求b、c的值;
(2)若函数y1+y2的图象与x轴始终有公共点,求直线l的解析式;
(3)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB为等腰角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
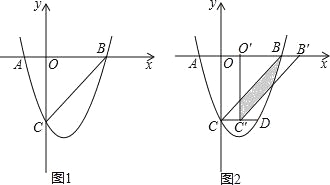
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于点A(﹣1,0),B(3,0)、C(0,﹣3)三点.
(1)直接写出抛物线的解析式 ;
(2)点D(2,m)在第一象限的抛物线上,连接BC、BD,试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由.
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′,在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒(0≤t≤3),试求S与t之间的函数关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2017年实现生产总值达280亿的目标,用科学记数法表示“280亿”为( )
A. 28×109 B. 2.8×108 C. 2.8×109 D. 2.8×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,其中正确的个数是( )
(1)有理数中,有绝对值最小的数;(2)有理数不是整数就是分数;(3)当a表示正有理数,则-a一定是负数;(4)a是大于-1的负数,则a2小于a3
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林城市对教师试卷讲评课中学生参与的深度与广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
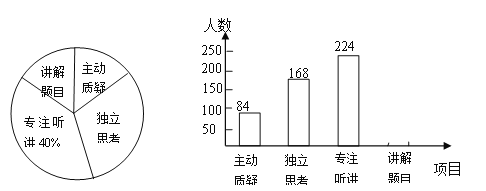
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形图补充完整;
(3)如果全市有16万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农大毕业的小王回乡自主创业,在大棚中栽培新品种的蘑菇,该种蘑菇在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培,每天只开启一次,如图是某天恒温系统从开启升温到保持恒温及关闭.大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是函数y=![]() (k>0)图象的一部分.若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间为( )
(k>0)图象的一部分.若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间为( )
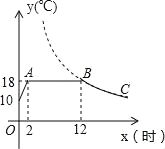
A.18小时 B.17.5小时 C.12小时 D.10小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com