
 ,且图象向右平移一个单位后经过坐标原点O.
,且图象向右平移一个单位后经过坐标原点O.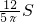 ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.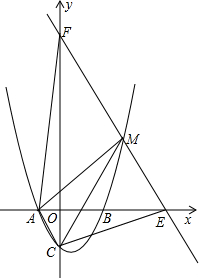 解:(1)∵抛物线的对称轴是直线x=
解:(1)∵抛物线的对称轴是直线x=
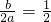

 ,-
,- )
) ,
, ,
,
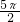 ,
,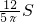 =6,
=6, CF•OA=6,
CF•OA=6, AE•OC=6
AE•OC=6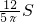 ,且M1(3,4),M2(-4,18).
,且M1(3,4),M2(-4,18). ,过点(-1,0),可确定二次函数y=ax2-x+c的待定系数a、c,确定解析式;
,过点(-1,0),可确定二次函数y=ax2-x+c的待定系数a、c,确定解析式;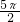 ,故S△ACM=
,故S△ACM=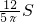 =6,用面积法可求满足S△ACM=6的M点所在的直线EF的解析式,再与抛物线联立,得出满足题意的点M.
=6,用面积法可求满足S△ACM=6的M点所在的直线EF的解析式,再与抛物线联立,得出满足题意的点M.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| AO |
| 1 |
| OB |
| 2 |
| CO |
查看答案和解析>>
科目:初中数学 来源: 题型:
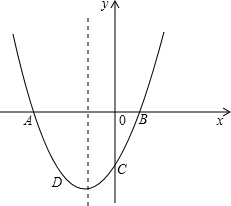 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.查看答案和解析>>
科目:初中数学 来源: 题型:
| x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 3 | 0 | -1 | 0 | m | 8 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com