
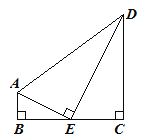
【题目】如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB·AD;
(3)若AB=1,CD=4,求线段AD,DE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)10.
【解析】试题分析:(1)根据垂直的定义和直角三角形的性质,求出∠BAE=∠CED,然后利用两角对应相等的两三角形相似可证;
(2)根据相似三角形的性质:相似三角形的对应边成比例,以及两边对应成比例且夹角相等的两三角形相似,可证明结论;
(3)根据相似三角形的性质,由(2)的结论△ABE∽△AED得到对应边成比例,然后根据勾股定理求解.
试题解析:(1)证明:∵AE⊥DE,∴∠AED=90°,∴∠AEB+∠CED=180°-90°=90°,
∵∠ABC=90°,∴∠BAE+∠AEB=90°,∴∠BAE=∠CED.
又∵∠ABC=∠BCD,∴△ABE∽△ECD.
(2) ∵△ABE∽△ECD,∴ ![]() .
.
∵点E为BC的中点,∴BE=EC.
∴![]() .
.
又∵∠ABC=∠AED=90°,∴△ABE∽△AED,
∴![]() ,∴AE2=AB·AD.
,∴AE2=AB·AD.
(3)∵△ABE∽△ECD,∴ ![]() .
.
∵AB=1,CD=4,BE=EC,∴BE2=AB·CD=4.
由勾股定理,得AE2=AB2+ BE2=5.
∵AE2=AB·AD,∴![]() .
.
由勾股定理,得![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
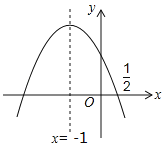
【题目】(4分)如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式的化简后,遇到了这样一个需要化简的式子:![]() .该如何化简呢?思考后,他发现3+2
.该如何化简呢?思考后,他发现3+2![]() =1+2
=1+2![]() +(
+(![]() )2=(1+
)2=(1+![]() )2.于是
)2.于是![]() =
=![]() =1+
=1+![]() .善于思考的小明继续深入探索;当a+b
.善于思考的小明继续深入探索;当a+b![]() =(m+n
=(m+n![]() )2时(其中a,b,m,n均为正整数),则a+b
)2时(其中a,b,m,n均为正整数),则a+b![]() =m2+2
=m2+2![]() mn+2n2.此时,a=m2+2n2,b=2mn,于是,
mn+2n2.此时,a=m2+2n2,b=2mn,于是,![]() =m+n
=m+n![]() .请你仿照小明的方法探索并解决下列问题:
.请你仿照小明的方法探索并解决下列问题:
(1)设a,b,m,n均为正整数且![]() =m+n
=m+n![]() ,用含m,n的式子分别表示a,b时,结果是a= ,b= ;
,用含m,n的式子分别表示a,b时,结果是a= ,b= ;
(2)利用(1)中的结论,选择一组正整数填空:![]() = +
= + ![]() ;
;
(3)化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
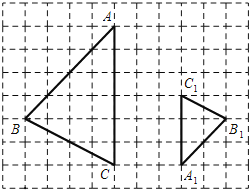
【题目】如图,在![]() 网格图中,
网格图中,![]() 与
与![]() 是位似图形.
是位似图形.
![]() 若在网格上建立平面直角坐标系,使得点A的坐标为
若在网格上建立平面直角坐标系,使得点A的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,写出点B的坐标;
,写出点B的坐标;
![]() 以点A为位似中心,在网格图中作
以点A为位似中心,在网格图中作![]() ,使
,使![]() 和
和![]() 位似,且位似比为1:2;
位似,且位似比为1:2;
![]() 在图上标出
在图上标出![]() 与
与![]() 的位似中心P,并写出点P的坐标,计算四边形ABCP的周长.
的位似中心P,并写出点P的坐标,计算四边形ABCP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,连接
上的点,连接![]() ,
,![]() ,
,![]() .
.

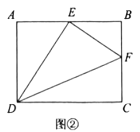
(1)如图①,当![]() 时,试说明
时,试说明![]() 是直角三角形;
是直角三角形;
(2)如图②,若点![]() 是边
是边![]() 的中点,
的中点,![]() 平分
平分![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com