
【题目】如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_________处。(填数字)

【答案】4
【解析】
由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点满足条件;如图:点P是△ABC两条外角平分线的交点,
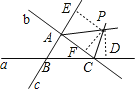
过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4个.
故答案是:4.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面坐标系中,![]() 为原点,直线
为原点,直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .
.
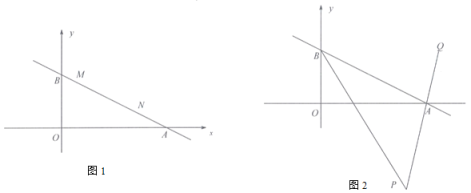
(1) 如图1,直线![]() 上有
上有![]() 和
和![]() 两点,
两点,![]() 的相反数是
的相反数是![]() ,
,![]() 是
是![]() 的算术平方根,求:
的算术平方根,求:
①![]() ____ ;
____ ; ![]() _____ ; ②点
_____ ; ②点![]() 在
在![]() 轴正半轴上运动,使得
轴正半轴上运动,使得![]() ,则点
,则点![]() 的坐标为 .
的坐标为 .
(2)如图2, 若![]() 的平分线
的平分线![]() 与
与![]() 的平分线
的平分线![]() 反向延长线交于点
反向延长线交于点![]() ,设
,设![]() ,求证:
,求证:![]() 的值为定值;
的值为定值;
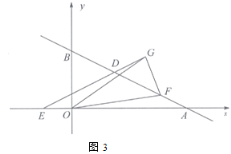
(3)如图3,![]() 在直线
在直线![]() 上,
上, ![]() 在
在![]() 轴上,在
轴上,在![]() 中,始终满足以下条件:
中,始终满足以下条件:![]() 为最大边,
为最大边, ![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
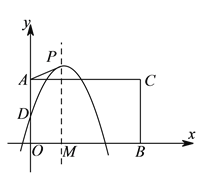
【题目】如图,在平面直角坐标系中,点![]() ,
, ![]() 分别是
分别是![]() 轴正半轴,
轴正半轴, ![]() 轴正半轴上两动点,
轴正半轴上两动点, ![]() ,
, ![]() ,以
,以![]() ,
, ![]() 为邻边构造矩形
为邻边构造矩形![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
, ![]() 为顶点,
为顶点, ![]() 轴于点
轴于点![]() .
.
(![]() )求
)求![]() ,
, ![]() 的长(结果均用含
的长(结果均用含![]() 的代数式表示);
的代数式表示);
(![]() )当
)当![]() 时,求该抛物线的表达式;
时,求该抛物线的表达式;
(![]() )在点
)在点![]() 在整个运动过程中,若存在
在整个运动过程中,若存在![]() 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 E 在 AD 的延长线上,下列条件中能判断 AB∥CD 的是( )

A. ∠1=∠4B. ∠2=∠3C. ∠C=∠CDED. ∠C+∠CDA=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A2017的坐标是( )
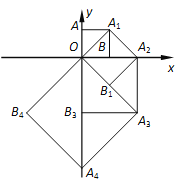
A. (0,21008) B. (21008,21008) C. (21009,0) D. (21009,-21009)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,AB∥CD,点 E 在 AB 上,点 M 在 CD 上,点 F 在直线 AB,CD 之间,连接 EF、FM, EF⊥FM,∠CMF=140°.
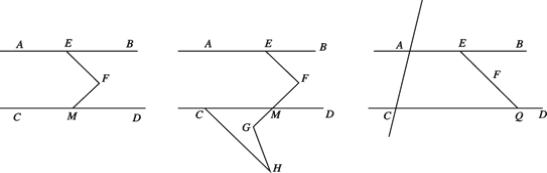
图 1 图 2 图 3
(1)直接写出∠AEF 的度数为 ________;
(2)如图 2,延长 FM 到 G,点 H 在 FG 的下方,连接 GH,CH,若∠FGH=∠H+90°, 求∠MCH 的度数;
(3)如图 3,作直线 AC,延长 EF 交 CD 于点 Q,P 为直线 AC 上一动点,探究∠PEQ,∠PQC 和∠EPQ 的数量关系,请直接给出结论.(题中所有角都是大于 0°小于 180°的角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2![]() x+m=0有两个不相等的实数根.
x+m=0有两个不相等的实数根.
(1)求实数m的最大整数值;
(2)在(1)的条件下,方程的实数根是x1,x2,求代数式![]() +
+![]() -
-![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com