
【题目】在平面坐标系中,![]() 为原点,直线
为原点,直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .
.
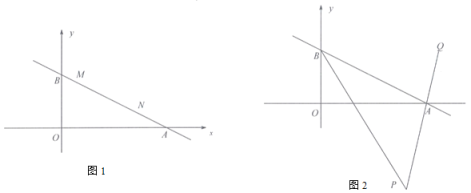
(1) 如图1,直线![]() 上有
上有![]() 和
和![]() 两点,
两点,![]() 的相反数是
的相反数是![]() ,
,![]() 是
是![]() 的算术平方根,求:
的算术平方根,求:
①![]() ____ ;
____ ; ![]() _____ ; ②点
_____ ; ②点![]() 在
在![]() 轴正半轴上运动,使得
轴正半轴上运动,使得![]() ,则点
,则点![]() 的坐标为 .
的坐标为 .
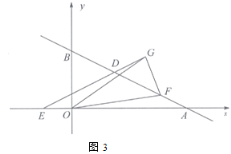
(2)如图2, 若![]() 的平分线
的平分线![]() 与
与![]() 的平分线
的平分线![]() 反向延长线交于点
反向延长线交于点![]() ,设
,设![]() ,求证:
,求证:![]() 的值为定值;
的值为定值;
(3)如图3,![]() 在直线
在直线![]() 上,
上, ![]() 在
在![]() 轴上,在
轴上,在![]() 中,始终满足以下条件:
中,始终满足以下条件:![]() 为最大边,
为最大边, ![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ;②
;②![]() 或
或![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 的取值范围是
的取值范围是![]()
【解析】
(1)①根据相反数和算数平方根的定义进行解题, ②分两种情况进行讨论即可解题,见详解,
(2)利用外角的性质即可解题,
(3)设![]() 为
为![]() ,利用
,利用![]() 得到OF=OG,进而得到
得到OF=OG,进而得到![]() 再由外角的性质得到
再由外角的性质得到![]() ,根据
,根据![]() ,和三角形的内角和即可求解.
,和三角形的内角和即可求解.
(1)①∵![]() 的相反数是
的相反数是![]() ,
,![]() 是
是![]() 的算术平方根,
的算术平方根,
∴![]()
②设直线AB的为y=kx+b(k≠0),
将M(1,3),N(5,1)代入得
K=![]() ,b=
,b=![]()
∴![]()
令y=0,得A(7,0),
设C(x,0)如下图,
当C在直线MN左侧时,S△MNC1=S△AMC1-S△ANC1=![]() ,解得:x=1,∴
,解得:x=1,∴![]()
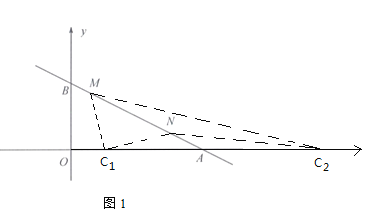
当C在直线MN右侧时,S△MNC2=S△AMC2-S△ANC2=![]() ,解得:x=13,∴
,解得:x=13,∴![]()
综上,![]() 或
或![]()
(2)证明:设![]() ,
,
![]()
![]()
![]()
![]() 的值为定值
的值为定值
(3)设![]() 为
为![]()
![]() ,
,![]() ,
,![]() ,OF=OG,
,OF=OG,
![]() ,
,![]()
![]()
![]()
![]() 为最大边,
为最大边,![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() 的取值范围是
的取值范围是![]()


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
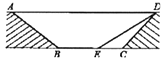
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面![]() 与通道
与通道![]() 平行),通道水平宽度
平行),通道水平宽度![]() 为8米,
为8米, ![]() ,通道斜面
,通道斜面![]() 的长为6米,通道斜面
的长为6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的长为 米;
的长为 米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面![]() 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面![]() 的坡角为30°,求此时
的坡角为30°,求此时![]() 的长.(结果保留根号)
的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
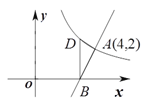
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]()
![]() 轴交反比例函数的图象于点
轴交反比例函数的图象于点![]() ,求点D的坐标和
,求点D的坐标和![]() 的面积;
的面积;
(3)观察图象,写出当x>0时不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知点M(1,4),N(5,2),P(0,3),Q(3,0),过P,Q两点的直线的函数表达式为y=﹣x+3,动点P从现在的位置出发,沿y轴以每秒1个单位长度的速度向上移动,设移动时间为ts.
(1)若直线PQ随点P向上平移,则:
①当t=3时,求直线PQ的函数表达式.
②当点M,N位于直线PQ的异侧时,确定t的取值范围.
(2)当点P移动到某一位置时,△PMN的周长最小,试确定t的值.
(3)若点P向上移动,点Q不动.若过点P,Q的直线经过点A(x0,y0),则x0,y0需满足什么条件?请直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[m]为不大于m的最大整数;
(1)填空:[3.2]= ,[﹣4.8]= ;
(2)已知:动点C在数轴上表示数a,且﹣2≤[a]≤4,则a的取值范围 ;
(3)如图:OB=1,AB⊥OB,且AB=10,动点D在数轴上表示的数为t,设AD﹣BD=n,且6≤[n]≤7,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日,是第23个世界读书日.为了推进中华传统文化教育,营造浓郁的读书氛围,我区某学校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此,特为每个班级订购了一批新的图书.初一年级两个班订购图书情况如下表:
老舍文集(套) | 四大名著(套) | 总费用(元) | |
初一(1)班 | 2 | 2 | 330 |
初一(2)班 | 3 | 2 | 380 |

(1)求老舍文集和四大名著每套各多少元?
(2)学校准备再购买老舍文集和四大名著共10套,总费用超过500元而不超过800元,问学校有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com