
����Ŀ��2019��4��23�գ��ǵ�23����������գ�Ϊ���ƽ��л���ͳ�Ļ�������Ӫ��Ũ���Ķ����Χ������ijѧУ�ٰ������ö����Ϊϰ�ߣ�������Ʈ��У��������Ϊ�ˣ���Ϊÿ���༶������һ���µ�ͼ�飮��һ�꼶�����ඩ��ͼ��������±���
�����ļ����ף� | �Ĵ��������ף� | �ܷ��ã�Ԫ�� | |
��һ��1���� | 2 | 2 | 330 |
��һ��2���� | 3 | 2 | 380 |

��1���������ļ����Ĵ�����ÿ������Ԫ��
��2��ѧУ���ٹ��������ļ����Ĵ�������10�ף��ܷ��ó���500Ԫ��������800Ԫ����ѧУ���ļ��ֹ�����
���𰸡���1�������ļ�ÿ��50Ԫ���Ĵ�����ÿ��115Ԫ����2������4�ֹ���������һ�����������ļ�6�ף��Ĵ�����4�ף������������������ļ�7�ף��Ĵ�����3�ף������������������ļ�8�ף��Ĵ�����2�ף������ģ����������ļ�9�ף��Ĵ�����1�ף�
��������
��1����������ͱ����е����ݿ����г���Ӧ�ķ����飬������Խ����
��2����������ͣ�1���еĽ�������г���Ӧ�IJ���ʽ�飬�Ӷ����Խ���⣮
�⣺��1���������ļ�ÿ��xԪ���Ĵ�����ÿ��yԪ����
![]() ��
��
��ã�![]() ��
��
�������ļ�ÿ��50Ԫ���Ĵ�����ÿ��115Ԫ��
��2����ѧУ���ٹ��������ļ�m�ף��Ĵ�������10��m���ף�
��500��50m+115��10��m����800��
��ã�5![]() ��m��10��
��m��10��
��x������
��x��6��7��8��9������4�ֹ�����
����һ�����������ļ�6�ף��Ĵ�����4�ף�
�����������������ļ�7�ף��Ĵ�����3�ף�
�����������������ļ�8�ף��Ĵ�����2�ף�
�����ģ����������ļ�9�ף��Ĵ�����1�ף�


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ������ϵ�У�![]() Ϊԭ�㣬ֱ��
Ϊԭ�㣬ֱ��![]() ��
��![]() ���������ڵ�
���������ڵ�![]() ����
����![]() ���������ڵ�
���������ڵ�![]() .
.
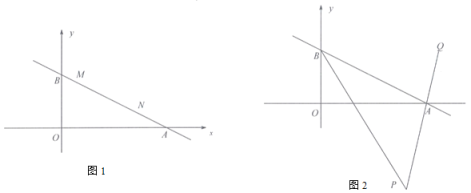
(1) ��ͼ1��ֱ��![]() ����
����![]() ��
��![]() ���㣬
���㣬![]() ���෴����
���෴����![]() ��
��![]() ��
��![]() ������ƽ����,��:
������ƽ����,��:
��![]() ____ ;
____ ; ![]() _____ ; �ڵ�
_____ ; �ڵ�![]() ��
��![]() �����������˶���ʹ��
�����������˶���ʹ��![]() ,���
,���![]() ������Ϊ .
������Ϊ .
(2)��ͼ2, ��![]() ��ƽ����
��ƽ����![]() ��
��![]() ��ƽ����
��ƽ����![]() �����ӳ��߽��ڵ�
�����ӳ��߽��ڵ�![]() ,��
,��![]() ,��֤:
,��֤:![]() ��ֵΪ��ֵ;
��ֵΪ��ֵ;
(3)��ͼ3,![]() ��ֱ��
��ֱ��![]() ��,
��, ![]() ��
��![]() ����,��
����,��![]() ��,ʼ��������������:
��,ʼ��������������:![]() Ϊ����,
����, ![]() ,��
,��![]() ʱ����
ʱ����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
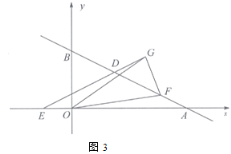
����Ŀ����ͼ 1��AB��CD���� E �� AB �ϣ��� M �� CD �ϣ��� F ��ֱ�� AB��CD ֮�䣬���� EF��FM�� EF��FM����CMF=140��.
ͼ 1 ͼ 2 ͼ 3
��1��ֱ��д����AEF �Ķ���Ϊ ________��
��2����ͼ 2���ӳ� FM �� G���� H �� FG ���·������� GH��CH������FGH=��H+90���� ���MCH �Ķ�����
��3����ͼ 3����ֱ�� AC���ӳ� EF �� CD �ڵ� Q��P Ϊֱ�� AC ��һ���㣬̽����PEQ����PQC �͡�EPQ ��������ϵ����ֱ�Ӹ�������.���������нǶ��Ǵ��� 0��С�� 180���Ľǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��P��B��C�ǰ뾶Ϊ8�ġ�O�ϵ��ĵ㣬�������BAC=��APC=60�㣬

��1����֤����ABC�ǵȱ������Σ�
��2����Բ��O��BC�ľ���OD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O������D��DE//AC����DE:AC=1��2������CE��OE������AE��OD�ڵ�F��
��1����֤��OE=CD��
��2��������ABCD�ı߳�Ϊ2����ABC=60������AE�ij���
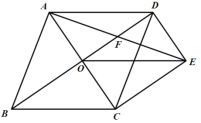
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������:
ͨ����ʽ����һ�µ�ѧϰ�����Ƿ���Ҫ��֤һ�����۵���ȷ�Կ��������ַ�����
���磺Ҫ��֤����![]()
����1������ͼ����֤������ͼ�����ǿ��Խ�һ���߳�Ϊ��a+b�����������ϲ�ȥһ���߳�Ϊ(a-b)��С��������ʣ��ͼ�ε����Ϊ4ab,��֤�ý�����ȷ��
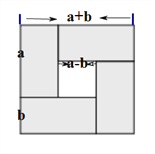
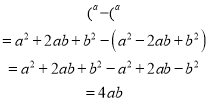
����2����������֤����ʽ���=![]() ��
��
���ԣ����=�ұߣ����۳�����
�۲����и�ʽ��
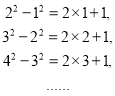
��1�������ɣ���д����n����ʽ________________��
��2)�Էֱ������ַ�����֤������۵���ȷ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�������̳�����һ�ָߵ�ˮ������ÿǧ��ӯ��10Ԫ��ÿ����۳�500ǧ�ˣ����г����鷢�֣��ڽ����۲��������£���ÿǧ���Ǽ�1Ԫ����������������20ǧ�ˣ��ָ��̳�Ҫ��֤ÿ��ӯ��6000Ԫ��ͬʱ��Ҫʹ�˿͵õ�ʵ�ݣ���
��1��ÿǧ��Ӧ�Ǽ۶���Ԫ��
��2����ˮ�������ۣ���ÿ��30�죩�Ƕ���ǧ�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2![]() x��m��0����������ȵ�ʵ������
x��m��0����������ȵ�ʵ������
(1)��ʵ��m���������ֵ��
(2)��(1)�������£����̵�ʵ������x1��x2�������ʽ![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
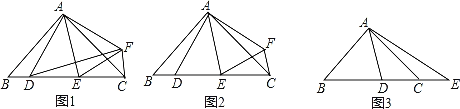
����Ŀ���ڡ�ABC�У�AB=AC����BAC=2��DAE=2����
��1����ͼ1������D����ֱ��AE�ĶԳƵ�ΪF����֤����ADF�ס�ABC��
��2����ͼ2���ڣ�1���������£�����=45�㣬��֤��DE2=BD2+CE2��
��3����ͼ3������=45�㣬��E��BC���ӳ����ϣ����ʽDE2=BD2+CE2���ܳ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com