
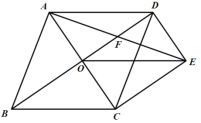
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE//AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
【答案】(1)证明见解析;(2)AE=![]() .
.
【解析】
(1)先证得OCED是平行四边形,再根据菱形的对角线互相垂直得到∠COD=90°,证得OCED是矩形,即可证明OE=CD;
(2)由菱形的性质和勾股定理求出AC与CE的长,最后根据勾股定理解答即可..
解:(1)∵在菱形ABCD中,
∴OC=![]() AC,AC⊥BD.
AC,AC⊥BD.
又∵DE:AC=1:2
∴DE=![]() AC
AC
∴DE=OC
∵DE//AC,
∴四边形OCED是平行四边形.
∵∠COD=90°
∴平行四边形OCED是矩形.
∴OE=CD
(2)∵在姜形ABCD中,
∴AB=BC=CD=AD=2,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2,AO=1.
∵在矩形OCED中,CE=OD=![]()
又∵矩形DOCE中,∠OCE=90°
∴在Rt△ACE中,AE=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有3个分别标有数字-1、1、2的小球,它们除标的数字不同外无其他区别.
(1)随机地从口袋中取出一小球,求取出的小球上标的数字为负数的概率;
(2)随机地从口袋中取出一小球,放回后再取出第二个小球,求两次取出的数字的和等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
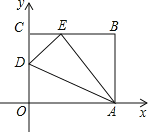
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日,是第23个世界读书日.为了推进中华传统文化教育,营造浓郁的读书氛围,我区某学校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此,特为每个班级订购了一批新的图书.初一年级两个班订购图书情况如下表:
老舍文集(套) | 四大名著(套) | 总费用(元) | |
初一(1)班 | 2 | 2 | 330 |
初一(2)班 | 3 | 2 | 380 |

(1)求老舍文集和四大名著每套各多少元?
(2)学校准备再购买老舍文集和四大名著共10套,总费用超过500元而不超过800元,问学校有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算F,规定:F(x,y)=ax+by(其中a,b均为非零常数).例如:F(3,4)=3a+4b.
(1)已知F(1,﹣1)=﹣1,F(2,0)=4.
①求a,b的值;
②已知关于p的不等式组![]() ,求p的取值范围;
,求p的取值范围;
(2)若运算F满足![]() ,请你直接写出F(m,m)的取值范围(用含m的代数式表示,这里m为常数且m>0).
,请你直接写出F(m,m)的取值范围(用含m的代数式表示,这里m为常数且m>0).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )

A.内部 B.外部 C.边上 D.以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,AB=AC=20cm,BD⊥AC于D,且BD=16cm.点M从点A出发,沿AC方向匀速运动,速度为4cm/s;同时点P由B点出发,沿BA方向匀速运动,速度为lcm/s,过点P的动直线PQ∥AC,交BC于点Q,连结PM,设运动时间为t(s)(0<t<5),解答下列问题:
(1)线段AD=___cm;
(2)求证:PB=PQ;
(3)当t为何值时,以P、Q、D、M为顶点的四边形为平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com