
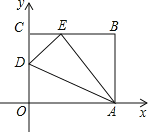
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是 .
【答案】(0,5)
【解析】
试题分析:先由矩形的性质得到AB=OC=8,BC=OA=10,再根据折叠的性质得AE=AO=10,DE=DO,在Rt△ABE中,利用勾股定理可计算出BE=6,则CE=BC﹣BE=4,设OD=x,则DE=x,DC=8﹣x,在Rt△CDE中根据勾股定理有x2=(8﹣x)2+42,解方程求出x,即可确定D点坐标.
解:∵四边形ABCD为矩形,
∴AB=OC=8,BC=OA=10,
∵纸片沿AD翻折,使点O落在BC边上的点E处,
∴AE=AO=10,DE=DO,
在Rt△ABE中,AB=8,AE=10,
∴BE=![]() =6,
=6,
∴CE=BC﹣BE=4,
设OD=x,则DE=x,DC=8﹣x,
在Rt△CDE中,∵DE2=CD2+CE2,
∴x2=(8﹣x)2+42,
∴x=5,
∴D点坐标为(0,5).
故答案为(0,5).


科目:初中数学 来源: 题型:
【题目】计算
(1)﹣5+3﹣2
(2)﹣20﹣(﹣18)+(﹣14)+13
(3)5.6+(﹣0.9)+4.4+(﹣8.1)
(4)(+ ![]() )﹣
)﹣![]() ﹣
﹣![]() +(﹣
+(﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
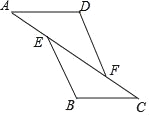
A. ∠D=∠B B. AD=CB C. BE=DF D. ∠AFD=∠CEB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) 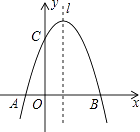
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
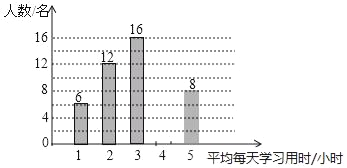
【题目】七中育才学校为调查本校学生周末平均每天学习所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分,请根据以上信息,解答下列问题:
(1)请把统计图补充完整;
(2)在这次调查的数据中,学习所用时间的众数是 ,中位数是 ,平均数是 ;
(3)若该校共有1000名学生,根据以上调查结果估计该校全体学生每天学习时间在3小时内(含3小时)的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用“同一个图形的面积用不同方式表示”可以证明一类含有线段的等式,这种解决问题的方法我们称之为等面积法.学有所用:在等腰三角形ABC中,AB=AC,其一腰上的高BD=h,M是底边BC上的任意一点,M到腰AB的距离ME=h1,M到腰AC的距离MF=h2.
(1)请你结合图形1来证明:h1+h2=h;
(2)当点M在BC的延长线上时,h1、h2、h之间又有什么样的结论,请你在图2中画出图形;
(3)请利用以上结论解答下列问题,如图3,在平面直角坐标系中有两条直线l1:y=![]() ,l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,求点M的坐标.
,l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )

A. 24 B. 28 C. 32 D. 36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com