
����Ŀ��������ͬһ��ͼ�ε�����ò�ͬ��ʽ��ʾ������֤��һ�ຬ���߶εĵ�ʽ�����ֽ������ķ������dz�֮Ϊ���������ѧ�����ã��ڵ���������ABC�У�AB=AC����һ���ϵĸ�BD=h��M�ǵױ�BC�ϵ�����һ�㣬M����AB�ľ���ME=h1��M����AC�ľ���MF=h2��
��1��������ͼ��1��֤����h1+h2=h��
��2������M��BC���ӳ�����ʱ��h1��h2��h֮������ʲô���Ľ��ۣ�������ͼ2�л���ͼ�Σ�
��3�����������Ͻ��۽���������⣬��ͼ3����ƽ��ֱ������ϵ��������ֱ��l1��y=![]() ��l2��y=��3x+3����l2�ϵ�һ��M��l1�ľ�����1�����M�����꣮
��l2��y=��3x+3����l2�ϵ�һ��M��l1�ľ�����1�����M�����꣮

���𰸡���1��h1+h2=h����2��h1��h2=h��ͼ�����������3����M������ΪM��![]() ��2����
��2����![]() ��4����
��4����
��������
��1������S��ABC=S��ABM+S��AMC��������𰸣�
��2��h1-h2=h��
��3���������ABCΪ���������Σ��ٸ��ݣ�1����2���Ľ���֢ٵ���M��BC����ʱ���ڵ���M��CB�ӳ�����ʱ�����M�����꣮�۵���M��BC���ӳ�����ʱ��h1=1��h�������ڣ�
��1������AM���������h1=ME��h2=MF��h=BD��
��S��ABC=S��ABM+S��AMC��
S��ABM=![]() ��AB��ME=
��AB��ME=![]() ��AB��h1��
��AB��h1��
S��AMC=![]() ��AC��MF=
��AC��MF=![]() ��AC��h2��
��AC��h2��
�֡�S��ABC=![]() ��AC��BD=
��AC��BD=![]() ��AC��h��AB=AC��
��AC��h��AB=AC��
��![]() ��AC��h=
��AC��h=![]() ��AB��h1+
��AB��h1+![]() ��AC��h2��
��AC��h2��
��h1+h2=h��
��2����ͼ��ʾ��

h1��h2=h��
��3����y=![]() x+3����x=0��y=3����y=0��x=��4��
x+3����x=0��y=3����y=0��x=��4��
����A����4��0����B��0��3��ͬ�����C��1��0����
AB=![]() =5��AC=5������AB=AC��
=5��AC=5������AB=AC��
����ABC����������
�ٵ���M��BC����ʱ����h1+h2=h�ã�1+My=OB��My=3��1=2��
��������y=��3x+3����ã�Mx=![]() ��
��
���Դ�ʱM��![]() ��2����
��2����
�ڵ���M��CB�ӳ�����ʱ����h1��h2=h�ã�My��1=OB��My=3+1=4��
��������y=��3x+3����ã�Mx=��![]() ��
��
���Դ�ʱM����![]() ��4����
��4����
�۵���M��BC���ӳ�����ʱ��h1=1��h�������ڣ�
������������M������ΪM��![]() ��2����
��2����![]() ��4����
��4����


 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90�㣬AC=BC=1������ABC�Ƶ�C��ʱ����ת�õ���A1B1C����ת��Ϊ����0�㣼����90�㣩������BB1 �� ��CB1��AB�ڵ�D��A1B1�ֱ�AB��AC�ڵ�E��F��
��1����֤����BCD�ա�A1CF��
��2������ת�Ǩ�Ϊ30�㣬
�������жϡ�BB1D����״��
����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
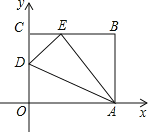
����Ŀ����ͼ��OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=10��OC=8����OC����ȡһ��D����ֽƬ��AD���ۣ�ʹ��O����BC���ϵĵ�E������D��������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������з���
��1��x2��5x��6=0
��2��2��x��3��2=8
��3��4x2��6x��3=0
��4����2x��3��2=5��2x��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l��![]() ��
��![]() �ύ�ڵ�A����ֱ��l�Ƶ�A˳ʱ����ת75������ֱ�ߵĽ���ʽΪ( )
�ύ�ڵ�A����ֱ��l�Ƶ�A˳ʱ����ת75������ֱ�ߵĽ���ʽΪ( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD��AC�ֱ���ֱ�����ң���CAD=30�㣬B��AC��һ�㣬BO��AD������ΪO��BO=5cm����CD����cm�� 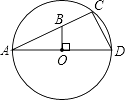
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A1��A2������An����ֱ��y=x-1�ϣ���B1��B2������Bn����˫����![]() �ϣ��������㣺A1B1��x�ᣬB1A2��y�ᣬA2B2��x�ᣬB2A3��y�ᣬ����AnBn��x�ᣬBnAn+1��y�ᣬ�����ǵ�An�ĺ�����Ϊan��nΪ������������a1=-1����a2016=______.
�ϣ��������㣺A1B1��x�ᣬB1A2��y�ᣬA2B2��x�ᣬB2A3��y�ᣬ����AnBn��x�ᣬBnAn+1��y�ᣬ�����ǵ�An�ĺ�����Ϊan��nΪ������������a1=-1����a2016=______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB�뺯��y��![]() ��x��0����ͼ���ڵ�A��m��2����B��2��n��������A��ACƽ����x�ύy���ڵ�C����y�Ḻ������ȡһ��D��ʹOD��
��x��0����ͼ���ڵ�A��m��2����B��2��n��������A��ACƽ����x�ύy���ڵ�C����y�Ḻ������ȡһ��D��ʹOD��![]() OC������ACD�������6������BC��
OC������ACD�������6������BC��
��1����m��k��n��ֵ��
��2������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ����ͨ��Դ�ͽ����Զ�����������ʱÿ��������10�棬���ȵ�100�棬ֹͣ���ȣ�ˮ�¿�ʼ�½�����ʱˮ��y���棩�뿪������ʱx��min���ɷ�������ϵ��ֱ��ˮ�½���20��ʱ�Զ��������ȣ��ظ������Զ���������ˮ��Ϊ20��ʱ����ͨ��Դ��ˮ��y���棩��ʱ��x��min���Ĺ�ϵ��ͼ��
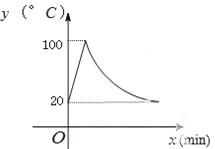
(1) �ֱ����ֱ��˫���ߵĽ���ʽ��
(2) ѧ����ÿ���¶������������ܺȵ�50������ˮ��ʱ���ж?
(3) ��ij������������ˮ���Զ���ͨ��Դ����ѧ�������һ���¿�ʱ��8��15���ܺȵ�����50���ˮ��˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com