
【题目】解下列方程
(1)x2﹣5x﹣6=0
(2)2(x﹣3)2=8
(3)4x2﹣6x﹣3=0
(4)(2x﹣3)2=5(2x﹣3)
【答案】
(1)解:原方程可化为:(x﹣6)(x+1)=0,
∴x﹣6=0或x+1=0,
∴x=6或x=﹣1
(2)解:方程两边同除以2,得:(x﹣3)2=4,
∴x﹣3=±2,
∴x﹣3=2或x﹣3=﹣2;
∴x1=5,x2=1
(3)解:∵a=4,b=﹣6,c=﹣3
∴△=b2﹣4ac=(﹣6)2﹣4×4×(﹣3)=84>0,
∴x= ![]() =
= ![]() =
= ![]() ,
,
∴x1= ![]() ,x2=
,x2= ![]()
(4)解:移项,得:(2x﹣3)2﹣5(2x﹣3)=0,
∴(2x﹣3)〔(2x﹣3)﹣5〕=0,
∴2x﹣3=0或2x﹣8=0,
∴x= ![]() 或x=4
或x=4
【解析】(1)因式分解法求解可得;(2)直接开平方法求解可得;(3)公式法求解可得;(4)因式分解法求解可得.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】在长方形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD﹣AB=2时,S2﹣S1的值为_______.(用a、b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) 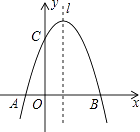
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
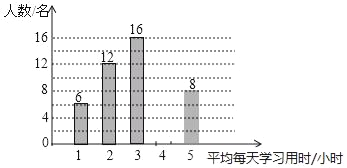
【题目】七中育才学校为调查本校学生周末平均每天学习所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分,请根据以上信息,解答下列问题:
(1)请把统计图补充完整;
(2)在这次调查的数据中,学习所用时间的众数是 ,中位数是 ,平均数是 ;
(3)若该校共有1000名学生,根据以上调查结果估计该校全体学生每天学习时间在3小时内(含3小时)的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
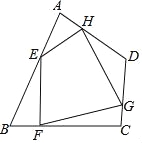
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用“同一个图形的面积用不同方式表示”可以证明一类含有线段的等式,这种解决问题的方法我们称之为等面积法.学有所用:在等腰三角形ABC中,AB=AC,其一腰上的高BD=h,M是底边BC上的任意一点,M到腰AB的距离ME=h1,M到腰AC的距离MF=h2.
(1)请你结合图形1来证明:h1+h2=h;
(2)当点M在BC的延长线上时,h1、h2、h之间又有什么样的结论,请你在图2中画出图形;
(3)请利用以上结论解答下列问题,如图3,在平面直角坐标系中有两条直线l1:y=![]() ,l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,求点M的坐标.
,l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )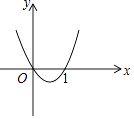
A.①④
B.②③④
C.③④⑤
D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠C=60°,我们把菱形ABCD的对称中心O称作菱形的中心.菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过1次这样的操作菱形中心O所经过的路径长为;经过3n(n为正整数)次这样的操作菱形中心O所经过的路径总长为 . (结果都保留π) 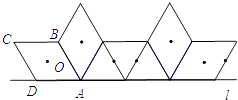
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com