
【题目】如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=______.
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=______.

【答案】![]() .
.
【解析】
根据题中所给已知条件可得A1的坐标为(-1,-2),B1的坐标为(-1,1),A2的坐标为(2,1),B2的坐标为![]() ,A3的坐标为
,A3的坐标为![]() ,B3的坐标为
,B3的坐标为![]() ,A4的坐标为(-1,-2),由此可知,从a1到an是按
,A4的坐标为(-1,-2),由此可知,从a1到an是按![]() 三个一组,循环出现的,由此即可求出a2016的值了.
三个一组,循环出现的,由此即可求出a2016的值了.
∵在直线y=x-1中,当x=a1=-1时,y=-2,
∴点A1的坐标为(-1,-2),
∵A1B1⊥x轴,点B1在反比例函数![]() 上,
上,
∴可得B1的坐标为(-1,1),
同理可得:A2的坐标为(2,1),B2的坐标为![]() ,A3的坐标为
,A3的坐标为![]() ,B4的坐标为
,B4的坐标为![]() ,A4的坐标为(-1,-2),……,
,A4的坐标为(-1,-2),……,
∴![]() ,……,
,……,
由此可知,从a1到an,每3个数组成一个循环,分别是![]() ,
,
∵2016÷3=672,
∴a2016是第672次循环的第三个数,
∴a2016=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
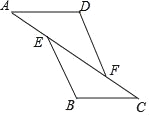
A. ∠D=∠B B. AD=CB C. BE=DF D. ∠AFD=∠CEB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用“同一个图形的面积用不同方式表示”可以证明一类含有线段的等式,这种解决问题的方法我们称之为等面积法.学有所用:在等腰三角形ABC中,AB=AC,其一腰上的高BD=h,M是底边BC上的任意一点,M到腰AB的距离ME=h1,M到腰AC的距离MF=h2.
(1)请你结合图形1来证明:h1+h2=h;
(2)当点M在BC的延长线上时,h1、h2、h之间又有什么样的结论,请你在图2中画出图形;
(3)请利用以上结论解答下列问题,如图3,在平面直角坐标系中有两条直线l1:y=![]() ,l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,求点M的坐标.
,l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )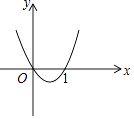
A.①④
B.②③④
C.③④⑤
D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于![]() 的长为半径画弧,两弧交于P,Q两点;
的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )

A. 24 B. 28 C. 32 D. 36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队甲、乙两名优秀队员在相同的条件下各射耙![]() 次,每次射耙的成绩情况如图所示:
次,每次射耙的成绩情况如图所示:

![]() 请将表格补充完整:
请将表格补充完整:
平均数 | 方差 | 中位数 | 命中 | |
甲 |
|
|
| |
乙 |
|
![]() 请从下列四个不同的角度对这次测试结果进行
请从下列四个不同的角度对这次测试结果进行
①从平均数和方差向结合看,________的成绩好些;
②从平均数和中位数相结合看,________的成绩好些;
③从平均数和折线统计图走势相结合看,________的成绩好些;
④若其他队选手最好成绩在![]() 环左右,现要选一人参赛,你认为选谁参加,并说明理由.
环左右,现要选一人参赛,你认为选谁参加,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com