
����Ŀ��ij������Ӽס������������Ա����ͬ�������¸����![]() �Σ�ÿ����ҵijɼ������ͼ��ʾ��
�Σ�ÿ����ҵijɼ������ͼ��ʾ��

![]() �뽫����������
�뽫����������
ƽ���� | ���� | ��λ�� | ���� | |
�� |
|
|
| |
�� |
|
![]() ��������ĸ���ͬ�ĽǶȶ���β��Խ������
��������ĸ���ͬ�ĽǶȶ���β��Խ������
�ٴ�ƽ�����ͷ������Ͽ���________�ijɼ���Щ��
�ڴ�ƽ��������λ�����Ͽ���________�ijɼ���Щ��
�۴�ƽ����������ͳ��ͼ�������Ͽ���________�ijɼ���Щ��
����������ѡ����óɼ���![]() �����ң���Ҫѡһ�˲���������Ϊѡ˭�μӣ���˵�����ɣ�
�����ң���Ҫѡһ�˲���������Ϊѡ˭�μӣ���˵�����ɣ�
���𰸡���1��![]() ��
��![]() ��
��![]() ��
��![]() ����2�����ף����ң����ң����ң�
����2�����ף����ң����ң����ң�
��������
��1���ֱ���ݷ��ʽ����λ���Ķ����Լ�����ƽ�����ļ��㷽�����м��㼴�ɵ�.��2���ֱ����ƽ�����������λ���������ɣ�
�⣻��1���ף�����=![]() [��9-7��2+��5-7��2+��7-7��2+��8-7��2+��7-7��2+��6-7��2+��8-7��2+��6-7��2+��7-7��2+��7-7��2]��
[��9-7��2+��5-7��2+��7-7��2+��8-7��2+��7-7��2+��6-7��2+��8-7��2+��6-7��2+��7-7��2+��7-7��2]��
=1.2��
�ɼ����մ�С�����˳���������£�5��6��6��7��7��7��7��7��8��8��9��
��5��6����������7��
���ԣ���λ����7��
����9�����ϵ���1����
�ң�ƽ����=![]() ��2+4+6+8+7+7+8+9+9+10��=
��2+4+6+8+7+7+8+9+9+10��=![]() ��70=7��
��70=7��
�ɼ����մ�С�����˳���������£�2��4��6��7��7��8��8��9��9��10��
��5������7����6������8��
���ԣ���λ����![]() ��7+8��=7.5��
��7+8��=7.5��
����9�����ϵ���3�Σ�
������£�
ƽ���� | ���� | ��λ�� | ����9�����ϵĻ��� | |
�� | 7 | 1.2 | 7 | 1 |
�� | 7 | 5.4 | 7.5 | 3 |
��2���ٴ�ƽ�����ͷ����Ͽ����ijɼ���Щ��
��Ϊ���ס��ҵ�ƽ����һ�������ķ���С���ɼ����Ҹ��ȶ���
�ڴ�ƽ��������λ�����Ͽ����ҵijɼ����ã�
��Ϊ�����˵�ƽ������ͬ���ҵ���λ�����ߣ�
�۴�ƽ����������9�����ϵĴ�����Ͽ����ҵijɼ���Щ��
��Ϊ���ס��ҵ�ƽ����һ�������ҵķ�����9�����ϵĴ�����3�Σ�����ֻ��1�Σ�
���ۺϿ������Ӹ��ȶ�����������Ȳ�ҷ����䲻�ȶ��������и߰л��������࣬�ɼ����DZ��������������ֵ��Ӧѡ�ң�


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A1��A2������An����ֱ��y=x-1�ϣ���B1��B2������Bn����˫����![]() �ϣ��������㣺A1B1��x�ᣬB1A2��y�ᣬA2B2��x�ᣬB2A3��y�ᣬ����AnBn��x�ᣬBnAn+1��y�ᣬ�����ǵ�An�ĺ�����Ϊan��nΪ������������a1=-1����a2016=______.
�ϣ��������㣺A1B1��x�ᣬB1A2��y�ᣬA2B2��x�ᣬB2A3��y�ᣬ����AnBn��x�ᣬBnAn+1��y�ᣬ�����ǵ�An�ĺ�����Ϊan��nΪ������������a1=-1����a2016=______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬��D��E�ֱ��DZ�BC��AB�ϵ��е㣬����DE���ӳ�����F��ʹEF=2DF������CE��AF��
��1��֤����AF=CE��
��2������B=30��ʱ�����ж��ı���ACEF����״��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ����ͨ��Դ�ͽ����Զ�����������ʱÿ��������10�棬���ȵ�100�棬ֹͣ���ȣ�ˮ�¿�ʼ�½�����ʱˮ��y���棩�뿪������ʱx��min���ɷ�������ϵ��ֱ��ˮ�½���20��ʱ�Զ��������ȣ��ظ������Զ���������ˮ��Ϊ20��ʱ����ͨ��Դ��ˮ��y���棩��ʱ��x��min���Ĺ�ϵ��ͼ��
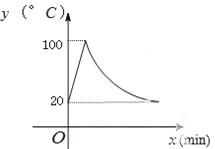
(1) �ֱ����ֱ��˫���ߵĽ���ʽ��
(2) ѧ����ÿ���¶������������ܺȵ�50������ˮ��ʱ���ж?
(3) ��ij������������ˮ���Զ���ͨ��Դ����ѧ�������һ���¿�ʱ��8��15���ܺȵ�����50���ˮ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���꼶���������![]() ����Ա���ڷ���Ͷ��ѵ���У���
����Ա���ڷ���Ͷ��ѵ���У���![]() ����Ա��Ͷ��
����Ա��Ͷ��![]() �εĽ���������±���
�εĽ���������±���
������ |
|
|
|
|
|
|
���� |
|
|
|
|
|
|
������ѵ���������������⣺
![]() ��
��![]() ����Ա��������ƽ������________����λ����________��
����Ա��������ƽ������________����λ����________��
![]() ����֧��ӷ��������ʣ�����������
����֧��ӷ��������ʣ�����������![]() ��������
��������![]() Ͷ��������
Ͷ��������![]() ________��
________��
![]() ����ԱС���ķ���������Ϊ
����ԱС���ķ���������Ϊ![]() ���������С������֧����еķ���ˮƽ��
���������С������֧����еķ���ˮƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=��m��2��x2+2mx+m+3��x�����������㣮
��1����m��ȡֵ��Χ��
��2����mȡ�����������������ʱ������������x����������������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�BD��ֱƽ��AC������Ϊ��F��EΪ�ı���ABCD��һ�㣬����ADE=��BAD��AE��AC��
��1����֤���ı���ABDE��ƽ���ı��Σ�
��2�����DAƽ����BDE��AB=5��AD=6����AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ6��B��������һ�㣬��AB=10������P�ӵ�A��������ÿ��6����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룬
��1��д�������ϵ�B����ʾ������ ����
��2����P����ʾ������ �������ú�t�Ĵ���ʽ��ʾ����
��3��M��AP���е㣬NΪPB���е㣬��P���˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯��˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��������ƽ�����ཻ�ڵ�I������I��DI��IC����AC�ڵ�D.
(1)��ͼ�٣���֤����AIB����ADI��
(2)��ͼ�ڣ��ӳ�BI������ǡ�ACE��ƽ�����ڵ�F.
���ж�DI��CF��λ�ù�ϵ����˵�����ɣ�
������BAC��70�������F�Ķ�����


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com