
【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


【答案】(1)证明见解析;(2)解:①结论:DI∥CF,②35°.
【解析】(1)只要证明∠AIB=90°+![]() ∠ACB,∠ADI=90°+
∠ACB,∠ADI=90°+![]() ∠ACB即可;
∠ACB即可;
(2)①只要证明∠IDC=∠DCF即可;
②首先求出∠ACE-∠ABC=∠BAC=70°,再证明∠F=![]() ∠ACE-
∠ACE-![]() ∠ABC=
∠ABC=![]() (∠ACE-∠ABC)即可解决问题;
(∠ACE-∠ABC)即可解决问题;
(1)证明:∵AI,BI分别平分∠BAC,∠ABC,
∴∠BAI=![]() ∠BAC,∠ABI=
∠BAC,∠ABI=![]() ∠ABC,
∠ABC,
∴∠BAI+∠ABI=![]() (∠BAC+∠ABC)=
(∠BAC+∠ABC)=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB.
∠ACB.
在△ABI中,∠AIB=180°-(∠BAI+∠ABI)=180°-(90°-![]() ∠ACB)=90°+
∠ACB)=90°+![]() ∠ACB.
∠ACB.
∵CI平分∠ACB,∴∠DCI=![]() ∠ACB.∵DI⊥IC,
∠ACB.∵DI⊥IC,
∴∠DIC=90°,∴∠ADI=∠DIC+∠DCI=90°+![]() ∠ACB.
∠ACB.
∴∠AIB=∠ADI.
(2)解:①结论:DI∥CF.
理由:∵∠IDC=90°-∠DCI=90°-![]() ∠ACB,CF平分∠ACE,
∠ACB,CF平分∠ACE,
∴∠ACF=![]() ∠ACE=
∠ACE=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB,∴∠IDC=∠ACF,∴DI∥CF.
∠ACB,∴∠IDC=∠ACF,∴DI∥CF.
②∵∠ACE=∠ABC+∠BAC,∴∠ACE-∠ABC=∠BAC=70°.
∵∠FCE=∠FBC+∠F,∴∠F=∠FCE-∠FBC.
∵∠FCE=![]() ∠ACE,∠FBC=
∠ACE,∠FBC=![]() ∠ABC,
∠ABC,
∴∠F=![]() ∠ACE-
∠ACE-![]() ∠ABC=
∠ABC=![]() (∠ACE-∠ABC)=35°.
(∠ACE-∠ABC)=35°.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】某市射击队甲、乙两名优秀队员在相同的条件下各射耙![]() 次,每次射耙的成绩情况如图所示:
次,每次射耙的成绩情况如图所示:

![]() 请将表格补充完整:
请将表格补充完整:
平均数 | 方差 | 中位数 | 命中 | |
甲 |
|
|
| |
乙 |
|
![]() 请从下列四个不同的角度对这次测试结果进行
请从下列四个不同的角度对这次测试结果进行
①从平均数和方差向结合看,________的成绩好些;
②从平均数和中位数相结合看,________的成绩好些;
③从平均数和折线统计图走势相结合看,________的成绩好些;
④若其他队选手最好成绩在![]() 环左右,现要选一人参赛,你认为选谁参加,并说明理由.
环左右,现要选一人参赛,你认为选谁参加,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是AB上一点,DF交AC于点E,FC∥AB,则下列结论错误的是( )

A. 若AE=CE,则DE=FE B. 若DE=FE,则AE=CE
C. 若BC=CF,则AD=CF D. 若AD=CF,则DE=FE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,E是BC的中点,以点A为中心,把△ABE逆时针旋转90°,设点E的对应点为F. 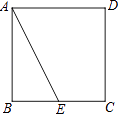
(1)画出旋转后的三角形.
(2)在(1)的条件下,
①求EF的长;
②求点E经过的路径弧EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】88层的金茂大厦的电梯上,有显示楼层的液晶屏,如图,可显示01,02,…,88,由于屏幕受到损坏,显示左边数字的7根线段中有1根不能亮了,显示右边数字的7根线段中有3根不能亮了。请问:电梯在运行的过程中,最多还有 _____个楼层的数字显示是正确的.

(说明)数字0、1、2、3、4、5、6、7、8、9显示方式如下图所示.

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.连接EG,判断EG与DF的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q).如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并且规定F(n)=![]() .例如18=1×18=2×9=3×6,这时就有F(18)=
.例如18=1×18=2×9=3×6,这时就有F(18)=![]() .请解答下列问题:
.请解答下列问题:
(1)计算:F(24);
(2)当n为正整数时,求证:F(n3+2n2+n)=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com