
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.连接EG,判断EG与DF的位置关系,并说明理由.

科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A. ①②④ B. ②③④
C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司向甲、乙两所中学送水,每次送往甲中学7600升,乙中学4000升.已知人均送水量相同,甲中学师生人数是乙中学的2倍少20人.
(1)求这两所中学师生人数分别是多少;
(2)若送瓶装水,价格为1元/升;若用消防车送饮用水,不需购买,但需配送水塔,容量500升的水塔售价为520元/个,其他费用不计.请问这次乙中学用瓶装水花费少还是饮用消防车送水花费少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的限距点的定义如下:若P′为直线PC与⊙C的一个交点,满足r≤PP′≤2r,则称P′为点P关于⊙C的限距点,如图为点P及其关于⊙C的限距点P′的示意图. 
(1)当⊙O的半径为1时.
①分别判断点M(3,4),N( ![]() ,0),T(1,
,0),T(1, ![]() )关于⊙O的限距点是否存在?若存在,求其坐标;
)关于⊙O的限距点是否存在?若存在,求其坐标;
②点D的坐标为(2,0),DE,DF分别切⊙O于点E,点F,点P在△DEF的边上.若点P关于⊙O的限距点P′存在,求点P′的横坐标的取值范围;
(2)保持(1)中D,E,F三点不变,点P在△DEF的边上沿E→F→D→E的方向运动,⊙C的圆心C的坐标为(1,0),半径为r,请从下面两个问题中任选一个作答.
问题1 | 问题2 |
若点P关于⊙C的限距点P′存在,且P′随点P的运动所形成的路径长为πr,则r的最小值为 | 若点P关于⊙C的限距点P′不存在,则r的取值范围为 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3 ![]() ,BG=4,则GH的长为 .
,BG=4,则GH的长为 . 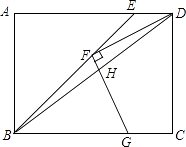
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中变形正确的是( )
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③![]() +
+![]() =4去分母,得3x+2x=24;
=4去分母,得3x+2x=24;
④(x+2)-2(x-1)=0去括号,得x+2-2x-2=0.
A. ①③ B. ①②③ C. ①④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com