
【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3 ![]() ,BG=4,则GH的长为 .
,BG=4,则GH的长为 . 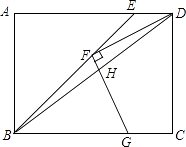
【答案】![]()
【解析】解:过点F作BC的垂线,分别交BC、AD于点M、N,则MN⊥AD,延长GF交AD于点Q,如图所示. ∵四边形ABCD是矩形,
∴∠ABC=90°,AD∥BC,
∵BE平分∠ABC,
∴∠ABE=∠EBC=45°,
∴△MBF是等腰直角三角形,
∵BF=3 ![]() ,
,
∴BM=FM=3,
∵BG=4,
∴MG=1,
∵FD⊥FG,
∴∠DFG=90°,
∴∠DFN+∠MFG=90°,
∵∠DNF=90°,
∴∠NDF+∠DFN=90°,
∴∠NDF=∠MFG,
在DNF和△FMG中, ,
,
∴△DNF≌△FMG(AAS),
∴DN=FM=3,NF=MG=1,
由勾股定理得:FG=FD= ![]() ,
,
∵QN∥BC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴FQ= ![]() ,QN=
,QN= ![]() ,
,
设GH=x,则FH= ![]() ﹣x,
﹣x,
∵QD∥AG,
∴ ![]() ,
,
∴ ![]() ,
,
x= ![]() ,
,
即GH= ![]() .
.
故答案为: ![]() .
.
作辅助线,构建相似三角形和全等三角形,先根据△ABF是等腰直角三角形求BM和FM的长,证明△DNF≌△FMG,得DN=FM=3,NF=MG=1;再利用AD∥BC和平行线分线段成比例定理依次列比例式,求QN和QF的长,设GH=x,列方程可求得GH的长.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,D是AB上一点,DF交AC于点E,FC∥AB,则下列结论错误的是( )

A. 若AE=CE,则DE=FE B. 若DE=FE,则AE=CE
C. 若BC=CF,则AD=CF D. 若AD=CF,则DE=FE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.连接EG,判断EG与DF的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论:w
①若a+b+c=0,且abc≠0,则方程a+bx+c=0的解是x=1;
②若a(x﹣1)=b(x﹣1)有唯一的解,则a≠b;
③若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=﹣![]() ;
;
④若a+b+c=1,且a≠0,则x=1一定是方程ax+b+c=1的解;
其中结论正确个数有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地。假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等,)又顺水航行返回万州,若该轮船从万州出发后所用时间为x(小时),轮船距万州的距离为y(千米),则下列各图中,能反映y与x之间函数关系的图象大致是【 】
A. B.
B.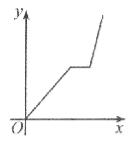 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学教材中数形结合的第一个实例,它包括原点,正方向和长度单位三要素,每一个实数都可以用数轴上的一个点来表示.
![]() 数轴上某一个点所对应的数为
数轴上某一个点所对应的数为![]() ,另一个点对应的数为
,另一个点对应的数为![]() ,则这两点之间的距离为________;
,则这两点之间的距离为________;
![]() 数轴上的数
数轴上的数![]() 对应的点为
对应的点为![]() ,点
,点![]() 位于
位于![]() 点的右边,距
点的右边,距![]() 点
点![]() 个长度单位,
个长度单位,![]() 为线段
为线段![]() 上的一点,
上的一点,![]() ,电子蚂蚁
,电子蚂蚁![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,相向而行,
同时出发,相向而行,![]() 的速度为
的速度为![]() 个长度单位/秒,
个长度单位/秒,![]() 的速度为
的速度为![]() 个长度单位/秒.
个长度单位/秒.
①当![]() 、
、![]() 距
距![]() 点距离相同时,求运动时间
点距离相同时,求运动时间![]() ;
;
②若电子蚂蚁![]() 通过
通过![]() 点
点![]() 秒后与电子蚂蚁
秒后与电子蚂蚁![]() 相遇,求
相遇,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q).如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并且规定F(n)=![]() .例如18=1×18=2×9=3×6,这时就有F(18)=
.例如18=1×18=2×9=3×6,这时就有F(18)=![]() .请解答下列问题:
.请解答下列问题:
(1)计算:F(24);
(2)当n为正整数时,求证:F(n3+2n2+n)=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com