
����Ŀ�������dz�����ѧ�̲������ν�ϵĵ�һ��ʵ����������ԭ�㣬������ͳ��ȵ�λ��Ҫ�أ�ÿһ��ʵ���������������ϵ�һ��������ʾ��
![]() ������ijһ��������Ӧ����Ϊ
������ijһ��������Ӧ����Ϊ![]() ����һ�����Ӧ����Ϊ
����һ�����Ӧ����Ϊ![]() ����������֮��ľ���Ϊ________��
����������֮��ľ���Ϊ________��
![]() �����ϵ���
�����ϵ���![]() ��Ӧ�ĵ�Ϊ
��Ӧ�ĵ�Ϊ![]() ����
����![]() �
λ��![]() ����ұߣ���
����ұߣ���![]() ��
��![]() �����ȵ�λ��
�����ȵ�λ��![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ�㣬
�ϵ�һ�㣬![]() ����������
����������![]() ��
��![]() �ֱ��
�ֱ��![]() ��
��![]() ͬʱ������������У�
ͬʱ������������У�![]() ���ٶ�Ϊ
���ٶ�Ϊ![]() �����ȵ�λ/�룬
�����ȵ�λ/�룬![]() ���ٶ�Ϊ
���ٶ�Ϊ![]() �����ȵ�λ/�룮
�����ȵ�λ/�룮
�ٵ�![]() ��
��![]() ��
��![]() �������ͬʱ�����˶�ʱ��
�������ͬʱ�����˶�ʱ��![]() ��
��
������������![]() ͨ��
ͨ��![]() ��
��![]() ������������
������������![]() ��������
��������![]() ��ֵ��
��ֵ��
![]()
���𰸡�(1)10; (2) ��![]() m��
m��![]() m����30.
m����30.
��������
��1�����������ľ��빫ʽ��⼴�ɣ���2���ٸ���P��Q��C�������ͬ���г����̿���ʱ��t���ڸ��ݵ�������Qͨ��C��1������������P��������ʱ��ĵ�����ϵ�г����̿���m��ֵ��
����1��2-��-8��=10��
��������֮��ľ���Ϊ10��
�ʴ�Ϊ��10��
��2������������![]() m-3t=
m-3t=![]() m-2t��
m-2t��
���t=![]() m��
m��
��3t+2t=m��
���t=![]() m��
m��
���˶�ʱ��tΪ![]() m��
m��![]() m��
m��
����������![]() ��
��
���m=30��
��m��ֵΪ30��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1+2+22+23+24+25+26��ֵʱ��С�����֣��ӵڶ���������ÿһ����������ǰһ��������2�����������裺S=1+2+22+23+24+25+26��Ȼ���ڢ�ʽ�����߶�����2���ã�2S=2+22+23+24+25+26+27 �ڣ��ک��ٵ�2S��S=27��1��S=27��1����1+2+22+23+24+25+26=27��1��
��1����1+3+32+33+34+35+36��ֵ��
��2����1+a+a2+a3+��+a2013��a��0��a��1����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���C�İ뾶Ϊr��P����Բ��C���غϵĵ㣬��P���ڡ�C�����Ķ������£���P��Ϊֱ��PC���C��һ�����㣬����r��PP���2r�����P��Ϊ��P���ڡ�C����㣬��ͼΪ��P������ڡ�C�����P���ʾ��ͼ�� 
��1������O�İ뾶Ϊ1ʱ��
�ٷֱ��жϵ�M��3��4����N�� ![]() ��0����T��1��
��0����T��1�� ![]() �����ڡ�O������Ƿ���ڣ������ڣ��������ꣻ
�����ڡ�O������Ƿ���ڣ������ڣ��������ꣻ
�ڵ�D������Ϊ��2��0����DE��DF�ֱ��С�O�ڵ�E����F����P�ڡ�DEF�ı��ϣ�����P���ڡ�O�����P����ڣ����P��ĺ������ȡֵ��Χ��
��2�����֣�1����D��E��F���㲻�䣬��P�ڡ�DEF�ı�����E��F��D��E�ķ����˶�����C��Բ��C������Ϊ��1��0�����뾶Ϊr���������������������ѡһ������
����1 | ����2 |
����P���ڡ�C�����P����ڣ���P�����P���˶����γɵ�·����Ϊ��r����r����СֵΪ | ����P���ڡ�C�����P�䲻���ڣ���r��ȡֵ��ΧΪ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�BEƽ�֡�ABC��AD�ڵ�E��FΪBE��һ�㣬����DF����F��FG��DF��BC�ڵ�G������BD��FG�ڵ�H����FD=FG��BF=3 ![]() ��BG=4����GH�ij�Ϊ ��
��BG=4����GH�ij�Ϊ �� 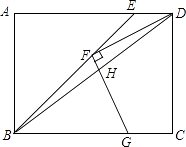
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬ֱ��AB�ֱ���x�ᡢy�ύ�ڵ�B��A���뷴����������ͼ����C��D��CE��x���ڵ�E����tan��ABO= ![]() ��OB=4��OE=2����D������Ϊ��6��m����
��OB=4��OE=2����D��������6��m���� 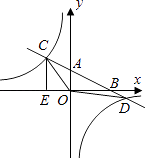
��1����ֱ��AB�ͷ����������Ľ���ʽ��
��2�����OCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ֻ����ռ�����![]() һ����������
һ����������![]() ������������ץס���ֻ��ᣬ���������������ܶ�ũ��ƷҲ�ı���ԭ��������ģʽ��ʵ�����������ۣ��ⲻ�մ�ѧ��ҵ��С�����ԼҵĶ����ƷҲ�ŵ������ϣ���ԭ�ƻ�ÿ����100�ﶬ�棬����������ԭ��ʵ��ÿ�����������ƻ�������г��룬�±���ij�ܵ��������
������������ץס���ֻ��ᣬ���������������ܶ�ũ��ƷҲ�ı���ԭ��������ģʽ��ʵ�����������ۣ��ⲻ�մ�ѧ��ҵ��С�����ԼҵĶ����ƷҲ�ŵ������ϣ���ԭ�ƻ�ÿ����100�ﶬ�棬����������ԭ��ʵ��ÿ�����������ƻ�������г��룬�±���ij�ܵ��������![]() �����Ϊ���������Ϊ��
����������������![]() �����
�����![]() ��
��
���� | һ | �� | �� | �� | �� | �� | �� |
��ƻ����IJ�ֵ |
|
|
|
|
|
|
|
(1)���ݼ�¼�����ݿ�֪ǰ���칲���� ______ �
(2)���ݼ�¼�����ݿ�֪����������һ������������ٵ�һ������� ______ �
(3)����ʵ�����������ﵽ�˼ƻ�����û�У�
(4)������ÿ�ﰴ8Ԫ���ۣ�ÿ�ﶬ����˷�ƽ��3Ԫ����ôС������һ���������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ尴��ͼ��ʾ�ķ�ʽ�ڷţ����С�ABCΪ����45��ǵ����ǰ壬ֱ��AD�ǵ���ֱ�����ǰ�ĶԳ��ᣬ��б���ϵĵ�DΪ��һ�����ǰ�DMN��ֱ�Ƕ��㣬DM��DN�ֱ�AB��AC�ڵ�E��F���������ĸ����ۣ���BD��AD��CD���ڡ�AED�ա�CFD����BE+CF��EF����S�ı���AEDF��![]() BC2��������ȷ������_____������ţ���
BC2��������ȷ������_____������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����з����б�����ȷ���ǣ� ��
��3x��6��0����Ϊx��2��0��
��2x��8��5��3x����Ϊx��3��
��![]() ��
��![]() ��4ȥ��ĸ����3x��2x��24��
��4ȥ��ĸ����3x��2x��24��
��(x��2)��2(x��1)��0ȥ���ţ���x��2��2x��2��0.
A. �٢� B. �٢ڢ� C. �٢� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��C��N������ͬһֱ���ϣ��ڡ�ABC�У���A����ABC����ACB=3��5��10������MNC�ա�ABC�����BCM����BCN=_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com