
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于点B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,若tan∠ABO= ![]() ,OB=4,OE=2,点D的坐标为(6,m).
,OB=4,OE=2,点D的坐标为(6,m). 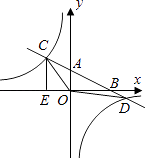
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
【答案】
(1)解:∵在直角△BCE中,tan∠ABO= ![]() =
= ![]() ,BE=OE+OB=4+2=6,
,BE=OE+OB=4+2=6,
∴EC=BEtan∠ABO=6× ![]() =3.
=3.
∴C的坐标是(﹣2,3).
设反比例函数的解析式是y= ![]() .
.
把C的坐标代入得:3= ![]() ,
,
解得:k=﹣6,
则反比例函数的解析式是:y=﹣ ![]()
B的坐标是(4,0).
∵在直角△AOB中,tan∠ABO= ![]() =
= ![]() ,
,
∴OA=OBtan∠ABO=4× ![]() =2,
=2,
则A的坐标是(0,2),
设直线AB的解析式是y=kx+b,
根据题意得: ![]() ,
,
解得: 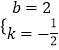 .
.
则直线AB的解析式是:y=﹣ ![]() x+2
x+2
(2)解:解方程组: 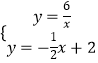 ,
,
解得: ![]() 或
或 ![]() ,
,
则D的坐标是:(6,﹣1).
∵OA=2
∴S△COD=S△OAC+S△OAD= ![]() ×2×2+
×2×2+ ![]() ×2×6=2+6=8
×2×6=2+6=8
【解析】(1)在直角△BCE中,BE=6,利用三角函数即可求得CE的长,则C的坐标即可求解,然后利用待定系数法即可求得反比例函数的解析式;(2)在直角△ABO中,利用三角函数即可求得OA的长,则A,B的坐标已知,利用待定系数法即可求得直线的解析式;(3)首先求得D的坐标,根据S△COD=S△OAC+S△OAD即可求解.
【考点精析】认真审题,首先需要了解解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)).


科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题.
饮水问题是关系到学生身心健康的重要生活环节,东坡中学共有教学班24个,平均每班有学生50人,经估算,学生一年在校时间约为240天(除去各种节假日),春、夏、秋、冬季各60天.原来,学生饮水一般都是购纯净水(其他碳酸饮料或果汁价格更高),纯净水零售价为1.5元/瓶,每个学生春、秋、冬季平均每天买1瓶纯净水,夏季平均每天要买2瓶纯净水,学校为了减轻学生消费负担,要求每个班自行购买1台冷热饮水机,经调查,购买一台功率为500 W的冷热饮水机约为150元,纯净水每桶6元,每班春、秋两季,平均每1.5天购买4桶,夏季平均每天购买5桶,冬季平均每天购买1桶,饮水机每天开10小时,当地民用电价为0.50元/度.
问题:
(1)在未购买饮水机之前,全年平均每个学生要花费多少钱来购买纯净水饮用?
(2)在购买饮水机解决学生饮水问题后,每班当年共要花费多少元?
(3)这项便利学生的措施实施后,东坡中学当年全体学生共节约多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=ax2﹣2(a﹣1)x+a﹣2(a>0).
(1)求证:抛物线与x轴有两个交点;
(2)设抛物线与x轴有两个交点的横坐标分别为x1 , x2 , (其中x1>x2).若y是关于a的函数,且y=ax2+x1 , 求这个函数的表达式;
(3)在(2)的条件下,结合函数的图象回答:若使y≤﹣3a2+1,则自变量a的取值范围为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论:w
①若a+b+c=0,且abc≠0,则方程a+bx+c=0的解是x=1;
②若a(x﹣1)=b(x﹣1)有唯一的解,则a≠b;
③若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=﹣![]() ;
;
④若a+b+c=1,且a≠0,则x=1一定是方程ax+b+c=1的解;
其中结论正确个数有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强居民节约用水意识,某市在2018年开始对供水范围内的居民用水实行“阶梯收费”,具体收费标准如下表:

某户居民四月份用水10 m3时,缴纳水费23元.
(1) 求a的值;
(2) 若该户居民五月份所缴水费为71元,求该户居民五月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学教材中数形结合的第一个实例,它包括原点,正方向和长度单位三要素,每一个实数都可以用数轴上的一个点来表示.
![]() 数轴上某一个点所对应的数为
数轴上某一个点所对应的数为![]() ,另一个点对应的数为
,另一个点对应的数为![]() ,则这两点之间的距离为________;
,则这两点之间的距离为________;
![]() 数轴上的数
数轴上的数![]() 对应的点为
对应的点为![]() ,点
,点![]() 位于
位于![]() 点的右边,距
点的右边,距![]() 点
点![]() 个长度单位,
个长度单位,![]() 为线段
为线段![]() 上的一点,
上的一点,![]() ,电子蚂蚁
,电子蚂蚁![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,相向而行,
同时出发,相向而行,![]() 的速度为
的速度为![]() 个长度单位/秒,
个长度单位/秒,![]() 的速度为
的速度为![]() 个长度单位/秒.
个长度单位/秒.
①当![]() 、
、![]() 距
距![]() 点距离相同时,求运动时间
点距离相同时,求运动时间![]() ;
;
②若电子蚂蚁![]() 通过
通过![]() 点
点![]() 秒后与电子蚂蚁
秒后与电子蚂蚁![]() 相遇,求
相遇,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=2AD, AH⊥BC于点H,E是CD的中点,连接AE、 BE、HE.
(1)求证: AE⊥BE
(2)求证:∠DEH=3 ∠ EHC

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下列程序计算,把答案填写在表格内,然后观察有什么规律,想一想:为什么会有这个规律?
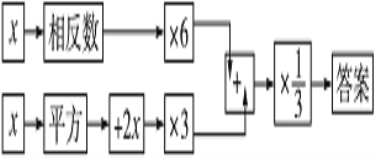
(1)填写表内空格:
输入 | -3 | -2 | -1 | 0 | … |
输出答案 | 9 |
|
|
| … |
(2)发现的规律是:输入数据x,则输出的答案是__________;
(3)为什么会有这个规律?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L1∥L2 , 圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于 . 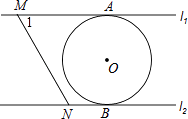
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com